强化学习-易混淆点
状态价值函数 vs 动作价值函数
状态价值函数
动作价值函数
优势函数
在状态 s 下选择动作 a 比平均情况（即遵循当前策略）好多少
A(s,a)=Q(s,a)−V(s)
- 求解优势函数：广义优势估计(GAE)
关系
常见强化学习算法优缺点
Q-Learning - Off-policy - 值函数
- 缺点：用表格存储动作价值。只在 环境的状态和动作都是离散的，并且空间都比较小 的情况下适用。
DQN - Off-policy - 值函数
适用于连续状态下离散动作的问题，可以使用ε-贪婪策略来平衡探索与利用。采用经验回放。
训练两个Q网络：训练网络 + 目标网络 —— 训练过程中 Q 网络的不断更新会导致目标不断发生改变，故暂时先将 TD 目标中的 Q 网络固定住。
- 缺点：仅限离散动作；训练资源消耗大；超参数敏感。
REINFORCE - 策略梯度
策略梯度
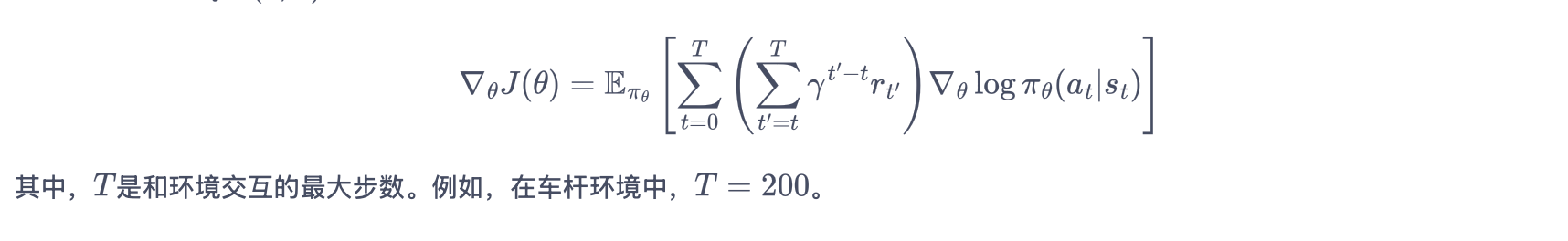
- 缺点：高方差；需大量样本；训练效率低
Actor-Critic - 策略+值函数
- 缺点：在实际应用过程中会遇到训练不稳定的情况。
TRPO -
常见强化学习算法的总结
算法 类型 适用场景 优势 劣势 Q-Learning 值函数（Off-policy） 离散动作、中小规模状态空间（如迷宫、简单游戏） 直接学习最优策略，无需遵循当前策略；实现简单 高估Q值风险；无法处理连续动作；高维状态需离散化 SARSA 值函数（On-policy） 离散动作、需安全探索的场景（如机器人避障） 策略保守，避免高风险动作；适合在线学习 可能收敛到局部最优；需遵循当前策略 DQN 值函数+深度网络 高维状态（如图像输入）、离散动作（如Atari游戏） 处理复杂状态；经验回放提高稳定性；适合端到端学习 仅限离散动作；训练资源消耗大；超参数敏感 REINFORCE 策略梯度（蒙特卡洛） 简单策略优化、连续或离散动作（如随机策略需求） 直接优化策略；支持连续动作 高方差；需大量样本；训练效率低 Actor-Critic 策略+值函数 连续/离散动作、需平衡方差与偏差（如机器人控制） 结合策略梯度与TD误差，收敛更快；支持在线更新 实现复杂；依赖Critic的准确性；需调参 PPO 策略优化（On-policy） 复杂连续/离散控制（如人形机器人、多智能体协作） 训练稳定（Clipping机制）；样本效率高；支持并行环境 超参数敏感（如Clipping范围）；计算资源需求较高 DDPG 确定性策略梯度（Off-policy） 高维连续动作空间（如无人机控制、精细操作） 输出确定性动作；适合精细控制；结合目标网络稳定训练 探索效率低（依赖噪声）；超参数敏感；对高维状态支持有限 TD3 确定性策略梯度改进版 复杂连续控制（DDPG的改进版） 缓解Q值高估（双Critic网络）；延迟策略更新提升稳定性 实现更复杂；训练时间较长 SAC 最大熵策略（Off-policy） 高维连续动作、需高探索性场景（如复杂物理仿真） 平衡探索与利用（熵正则化）；鲁棒性强；适合稀疏奖励任务 计算复杂度高；实现难度大 蒙特卡洛方法 无模型（On-policy/Off-policy） 回合制任务（如棋类游戏胜负评估） 无偏差；简单直观 高方差；需完整Episode；样本效率低 Dyna-Q 基于模型 已知或可学习模型的环境（如仿真调度、安全关键任务） 样本效率高；支持规划与学习结合 模型误差影响策略；复杂环境建模困难 A3C/A2C 异步策略梯度 分布式训练、并行环境交互（如多线程游戏AI） 加速训练（异步采样）；适合大规模计算资源 实现复杂；同步版本（A2C）效率较低