深度学习基础 - 激活函数和epoch, batch, iteration

写这篇文章有两个原因：一是因为我好久没看Activation Function又忘了，来复习一下；另一个是因为我想赶紧把这个风格的摄影作品用完，开启下一个系列 :)

引入激活函数的目的：加入非线性因素的，解决线性模型所不能解决的问题。通过最优化损失函数的做法，我们能够学习到不断学习靠近能够正确分类的曲线。

1 sigmoid 函数

sigmoid 函数是一个 logistic 函数：输入的每个神经元、节点或激活都会被缩放为一个介于 0 到 1 之间的值。

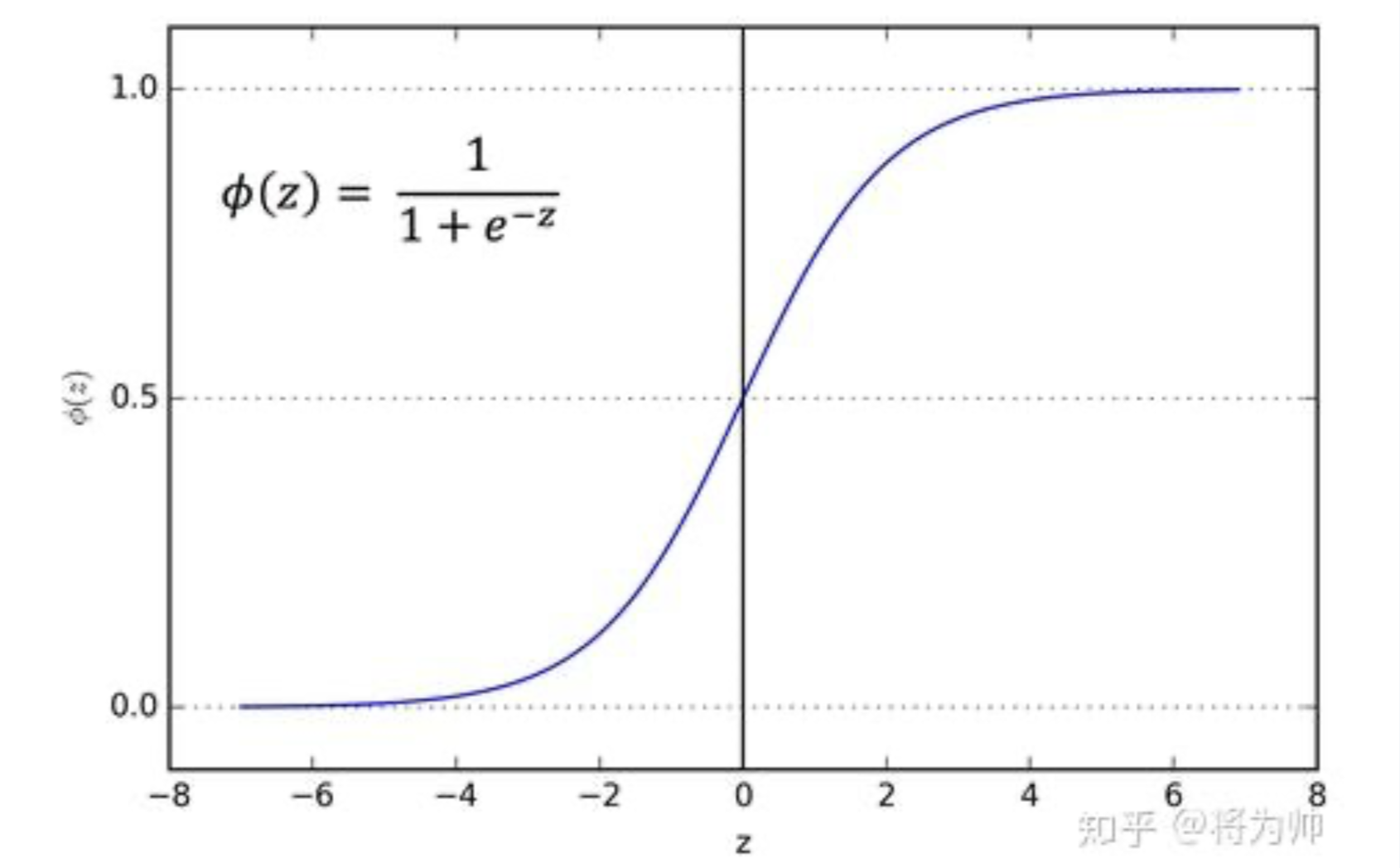
从图像可以看出，函数两个边缘的梯度约为0，梯度的取值范围为(0,0.25)：

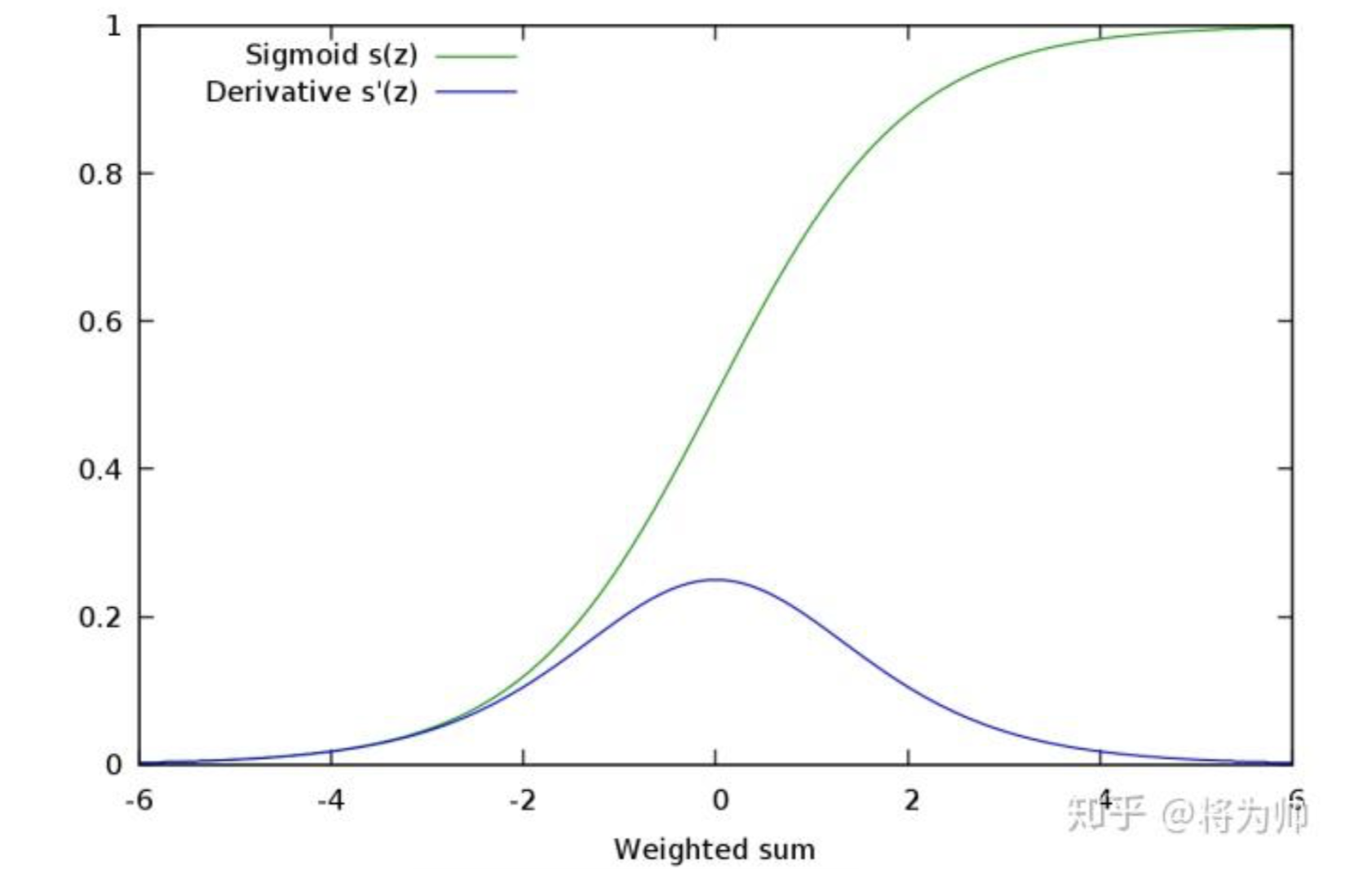
• 存在问题：梯度消失

  例如，一个网络由4个神经元线性组成，神经元的激活函数都为Sigmoid：

  

  当我们求激活函数输出相对于权重参数w的偏导时，Sigmoid函数的梯度是表达式中的一个乘法因子：

  

  以d对c的导数举例，展开如下：

  

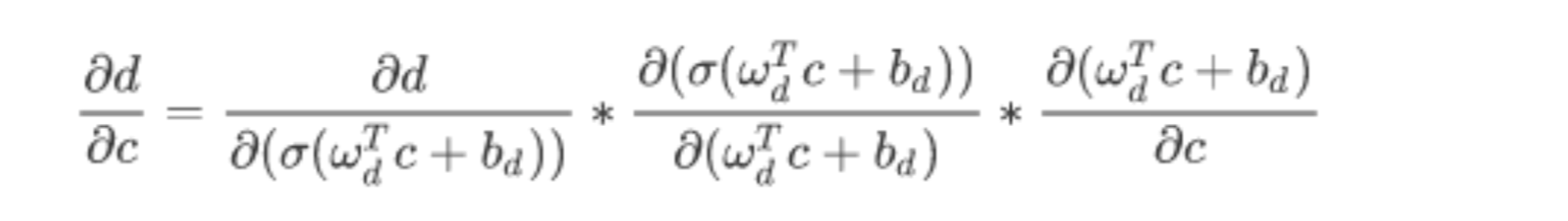
  式子的中间项是Sigmoid函数的梯度。

  即，拥有4个神经元的网络的Loss函数相对于第一层神经元a的偏导表达式中就包含4个Sigmoid梯度的乘积。

多个范围在(0,0.25)的数的乘积，将会是一个非常小的数字 —— 极小的梯度无法让参数得到有效更新。

2 ReLU 函数

ReLU激活函数的提出就是为了解决梯度消失问题。

ReLU的梯度只可以取两个值：0或1

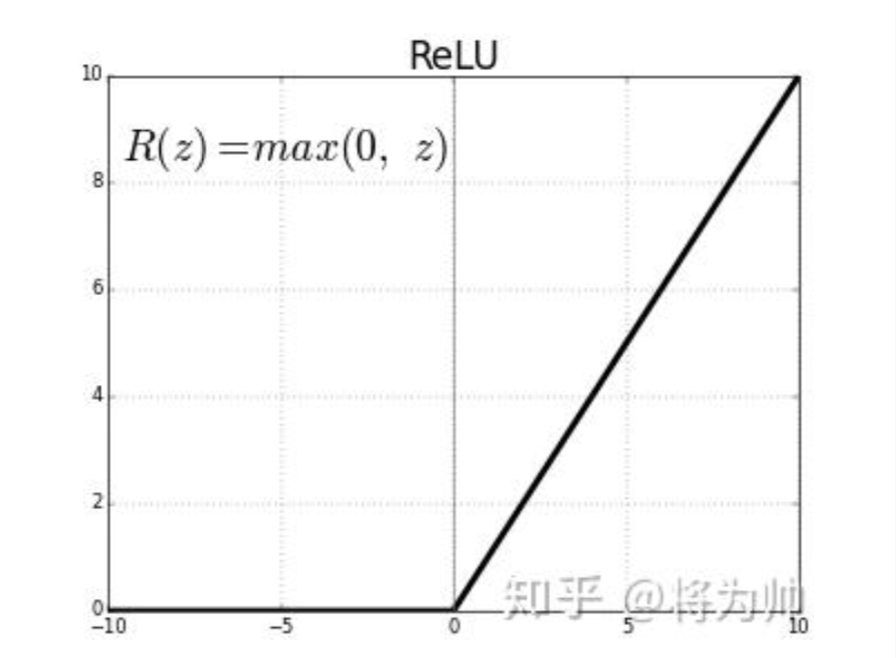
ReLU的梯度的连乘不会收敛到0 ，连乘的结果也只可以取两个值：0或1。

• 如果值为1，梯度保持值不变进行前向传播；
• 如果值为0，梯度从该位置停止前向传播。

单侧饱和

把神经元想象为检测某种特定特征的开关，高层神经元负责检测高级的/抽象的特征(有着更丰富的语义信息)，例如眼睛或者轮胎；低层神经元负责检测低级的/具象的特征，例如曲线或者边缘。

当开关处于开启状态，说明在输入范围内检测到了对应的特征，且正值越大代表特征越明显；用负值代表检测特征的缺失。

单侧饱和还能使得神经元对于噪声干扰更具鲁棒性。负值的大小引入了背景噪声或者其他特征的信息，会给后续的神经元带来无用的干扰信息；且可能导致神经元之间的相关性(重复信息)。在负值区域单侧饱和的神经元则不会有上述问题：噪声的程度大小被饱和区域都截断为0，避免了无用信息的干扰。

• 存在问题：神经元“死亡” (dying ReLU problem)

  激活函数的输入值有一项偏置项(bias)，假设bias变得太小，则输入激活函数的值总是负的，那么反向传播过程经过该处的梯度恒为0，对应的权重和偏置参数此次无法得到更新。

3 LeakyReLU

LeakyReLU可以解决神经元”死亡“问题。

LeakyReLU输入小于0的部分，值为负，且有微小的梯度。LeakyReLU的α取值一般为0.01。

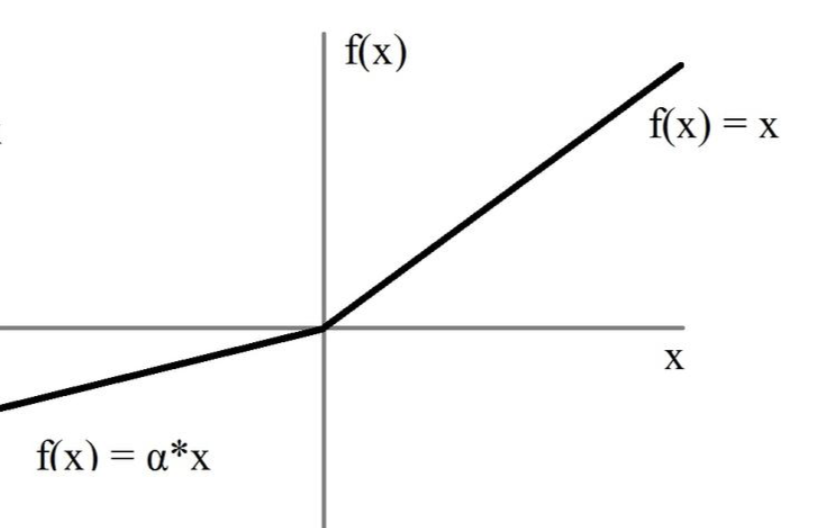
在反向传播过程中，对于LeakyReLU激活函数输入小于零的部分，也可以计算得到梯度(而不是像ReLU一样值为0)

如何选择合适的激活函数？

1. 先试试ReLU的效果如何。ReLU相较于其他激活函数，有着最低的计算代价和最简单的代码实现。

2. 如果ReLU效果不太理想，下一个建议是试试LeakyReLU或ELU。经验来看：有能力生成零均值分布的激活函数，相较于其他激活函数更优。

   需要注意的是使用ELU的神经网络训练和推理都会更慢一些，因为需要更复杂的指数运算得到函数激活值，如果计算资源不成问题，且网络并不十分巨大，可以事实ELU；否则，最好选用LeakyReLU。

3. 如果有很多算力或时间，可以试着对比下包括随机ReLU和PReLU在内的所有激活函数的性能。

   当网络表现出过拟合时，随机ReLU可能会有帮助。

   对PReLU来说，因为增加了需要学习的参数，当且仅当有很多训练数据时才可以试试PReLU的效果。

epoch, batch, iteration

一个epoch指的是把所有训练数据丢进神经网络一次。

由于训练数据常常太大了，不能够一口吃掉一个胖子，得慢慢来，所以我们常常把训练数据分成好几等份，分完之后每份数据的数量就是 batch size，而几等份的这个几就是iteration。

epoch：指的是次数，epoch = 10 指的是把整个数据集丢进神经网络训练10次。

batch size：指的是数据的个数，batch size = 10 指的是每次扔进神经网络训练的数据是10个。

iteration：同样指的是次数，iteration = 10 指的是把整个数据集分成10次扔进神经网络。

• Deep Learning