DQN (deep Q network)
Q-learning 算法用表格存储动作价值的做法只在 环境的状态和动作都是离散的,并且空间都比较小 的情况下适用.
DQN:用来解决连续状态下离散动作的问题,是离线策略算法,可以使用ε-贪婪策略来平衡探索与利用。
Q 网络:用于拟合函数Q函数的神经网络
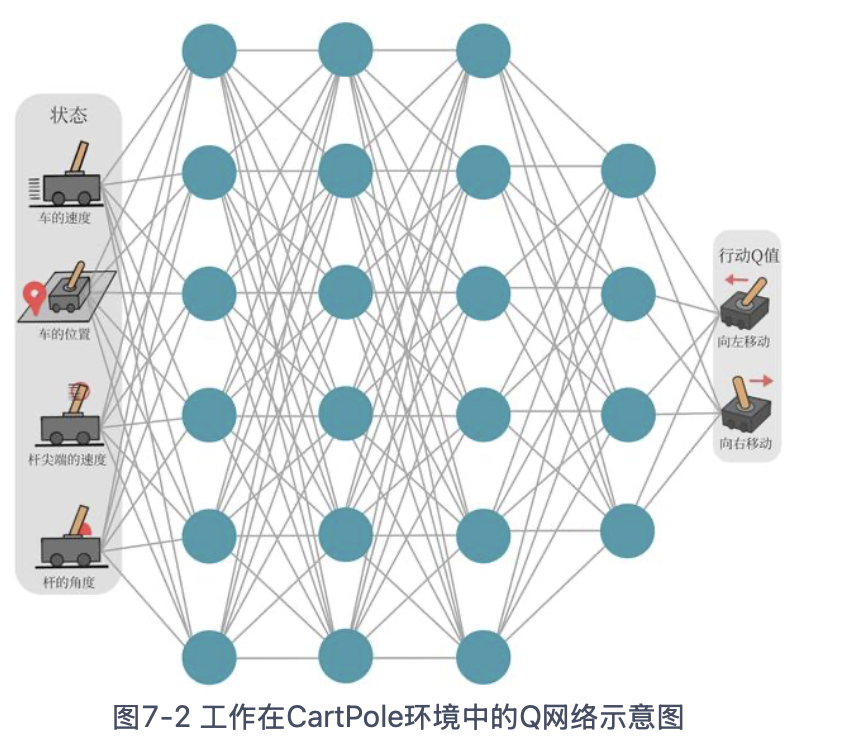
Q 网络的损失函数(均方误差形式)
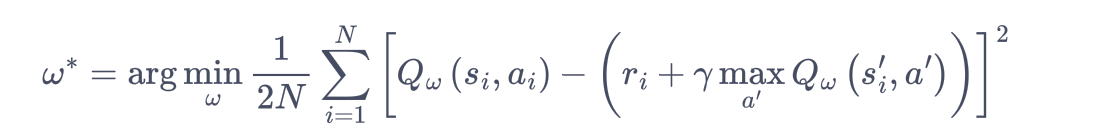
1. 经验回放模块
v.s Q-learning 算法:Q-learning 中每一个数据只会用来更新一次值。
经验回放(experience replay):
维护一个回放缓冲区,将每次从环境中采样得到的四元组数据(状态、动作、奖励、下一状态)存储到回放缓冲区中,训练 Q 网络的时候再从回放缓冲区中随机采样若干数据来进行训练。
作用:
使样本满足独立假设。
在 MDP 中交互采样得到的数据本身不满足独立假设,因为这一时刻的状态和上一时刻的状态有关。
非独立同分布的数据对训练神经网络有很大的影响,会使神经网络拟合到最近训练的数据上。采用经验回放可以打破样本之间的相关性,让其满足独立假设。
提高样本效率。
每一个样本可以被使用多次,适合深度神经网络的梯度学习。
2. 目标网络模块
目标网络(target network)核心思想:
训练过程中 Q 网络的不断更新会导致目标不断发生改变,故暂时先将 TD 目标中的 Q 网络固定住。
实现:两套 Q 网络 —— 训练网络 + 目标网络

3. DQN 算法
具体流程:

定义经验回放池的类,主要包括加入数据、采样数据两大函数。
class ReplayBuffer: ''' 经验回放池 ''' def __init__(self, capacity): self.buffer = collections.deque(maxlen=capacity) # 队列,先进先出 def add(self, state, action, reward, next_state, done): # 将数据加入buffer self.buffer.append((state, action, reward, next_state, done)) def sample(self, batch_size): # 从buffer中采样数据,数量为batch_size transitions = random.sample(self.buffer, batch_size) state, action, reward, next_state, done = zip(*transitions) return np.array(state), action, reward, np.array(next_state), done def size(self): # 目前buffer中数据的数量 return len(self.buffer)定义一个只有一层隐藏层的 Q 网络
class Qnet(torch.nn.Module): ''' 只有一层隐藏层的Q网络 ''' def __init__(self, state_dim, hidden_dim, action_dim): super(Qnet, self).__init__() self.fc1 = torch.nn.Linear(state_dim, hidden_dim) self.fc2 = torch.nn.Linear(hidden_dim, action_dim) def forward(self, x): x = F.relu(self.fc1(x)) # 隐藏层使用ReLU激活函数 return self.fc2(x)DQN 算法
class DQN:
''' DQN算法 '''
def __init__(self, state_dim, hidden_dim, action_dim, learning_rate, gamma,
epsilon, target_update, device):
self.action_dim = action_dim
self.q_net = Qnet(state_dim, hidden_dim,
self.action_dim).to(device) # Q网络
# 目标网络
self.target_q_net = Qnet(state_dim, hidden_dim,
self.action_dim).to(device)
# 使用Adam优化器
self.optimizer = torch.optim.Adam(self.q_net.parameters(),
lr=learning_rate)
self.gamma = gamma # 折扣因子
self.epsilon = epsilon # epsilon-贪婪策略
self.target_update = target_update # 目标网络更新频率
self.count = 0 # 计数器,记录更新次数
self.device = device
def take_action(self, state): # epsilon-贪婪策略采取动作
if np.random.random() < self.epsilon:
action = np.random.randint(self.action_dim)
else:
state = torch.tensor([state], dtype=torch.float).to(self.device)
action = self.q_net(state).argmax().item()
return action
def update(self, transition_dict):
states = torch.tensor(transition_dict['states'],
dtype=torch.float).to(self.device)
actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(
self.device)
rewards = torch.tensor(transition_dict['rewards'],
dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition_dict['next_states'],
dtype=torch.float).to(self.device)
dones = torch.tensor(transition_dict['dones'],
dtype=torch.float).view(-1, 1).to(self.device)
q_values = self.q_net(states).gather(1, actions) # Q值
# 下个状态的最大Q值
max_next_q_values = self.target_q_net(next_states).max(1)[0].view(
-1, 1)
q_targets = rewards + self.gamma * max_next_q_values * (1 - dones
) # TD误差目标
dqn_loss = torch.mean(F.mse_loss(q_values, q_targets)) # 均方误差损失函数
self.optimizer.zero_grad() # PyTorch中默认梯度会累积,这里需要显式将梯度置为0
dqn_loss.backward() # 反向传播更新参数
self.optimizer.step()
if self.count % self.target_update == 0:
self.target_q_net.load_state_dict(
self.q_net.state_dict()) # 更新目标网络
self.count += 1
训练
lr = 2e-3 num_episodes = 500 hidden_dim = 128 gamma = 0.98 epsilon = 0.01 target_update = 10 buffer_size = 10000 minimal_size = 500 batch_size = 64 device = torch.device("cuda") if torch.cuda.is_available() else torch.device( "cpu") env_name = 'CartPole-v0' env = gym.make(env_name) random.seed(0) np.random.seed(0) env.seed(0) torch.manual_seed(0) replay_buffer = ReplayBuffer(buffer_size) state_dim = env.observation_space.shape[0] action_dim = env.action_space.n agent = DQN(state_dim, hidden_dim, action_dim, lr, gamma, epsilon, target_update, device) return_list = [] for i in range(10): with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar: for i_episode in range(int(num_episodes / 10)): episode_return = 0 state = env.reset() done = False while not done: action = agent.take_action(state) next_state, reward, done, _ = env.step(action) replay_buffer.add(state, action, reward, next_state, done) state = next_state episode_return += reward # 当buffer数据的数量超过一定值后,才进行Q网络训练 if replay_buffer.size() > minimal_size: b_s, b_a, b_r, b_ns, b_d = replay_buffer.sample(batch_size) transition_dict = { 'states': b_s, 'actions': b_a, 'next_states': b_ns, 'rewards': b_r, 'dones': b_d } agent.update(transition_dict) return_list.append(episode_return) if (i_episode + 1) % 10 == 0: pbar.set_postfix({ 'episode': '%d' % (num_episodes / 10 * i + i_episode + 1), 'return': '%.3f' % np.mean(return_list[-10:]) }) pbar.update(1)
4. Dueling DQN 算法
1. 优势函数A(s,a)
在状态 s 下,选择动作 a 比平均情况(即遵循当前策略)好多少
A(s,a)=Q(s,a)−V(s)
- 定义:状态动作价值函数 减去 状态价值函数 的结果,表示采取不同动作的差异性。
- Q(s,a):表示在状态 s 下执行动作 a 后,未来能获得的总回报。
- V(s):表示在状态 s 下,遵循当前策略能获得的平均回报,即对所有可能的动作取期望。
2. Dueling DQN 中 Q 网络的建模


将状态价值函数和优势函数分别建模的好处:
去中心化,只关注动作的相对好坏。
某些情境下智能体只会关注状态的价值,而并不关心不同动作导致的差异;此时将二者分开建模能够使智能体更好地处理与动作关联较小的状态。
存在对于值V和值A建模不唯一性的问题,改进:强制最优动作的优势函数的实际输出为 0。
