PPO
1. 论文详读
Proximal Policy Optimization Algorithms(Proximal:近似)
2. PPO
回顾 TRPO
使用 KL 散度约束 policy 的更新幅度;使用重要性采样
缺点:近似会带来误差(重要性采样的通病);解带约束的优化问题困难
PPO 的改进
TRPO 采用重要性采样 —-> PPO 采用 clip 截断,限制新旧策略差异,避免更新过大。
优势函数 At 选用多步时序差分
自适应的 KL 惩罚项
Critic网络训练:
通过最小化
critic_loss = MSE(critic(states), td_target),让critic的价值估计更准确Actor网络更新:
- TD误差的广义形式(GAE)被用作优势函数,指导策略更新方向
- 优势函数越大,表示该动作比平均表现更好,应被加强
3. PPO-惩罚
PPO-惩罚(PPO-Penalty):用拉格朗日乘数法将 KL 散度的限制放进了目标函数中,使其变成了一个无约束的优化问题,在迭代的过程中不断更新 KL 散度前的系数 beta。

dk 即为 KL 散度值。
第一种情况 dk 小,说明安全,关注前项;第二种情况 dk 大,不安全,故乘 2 关注后一项。
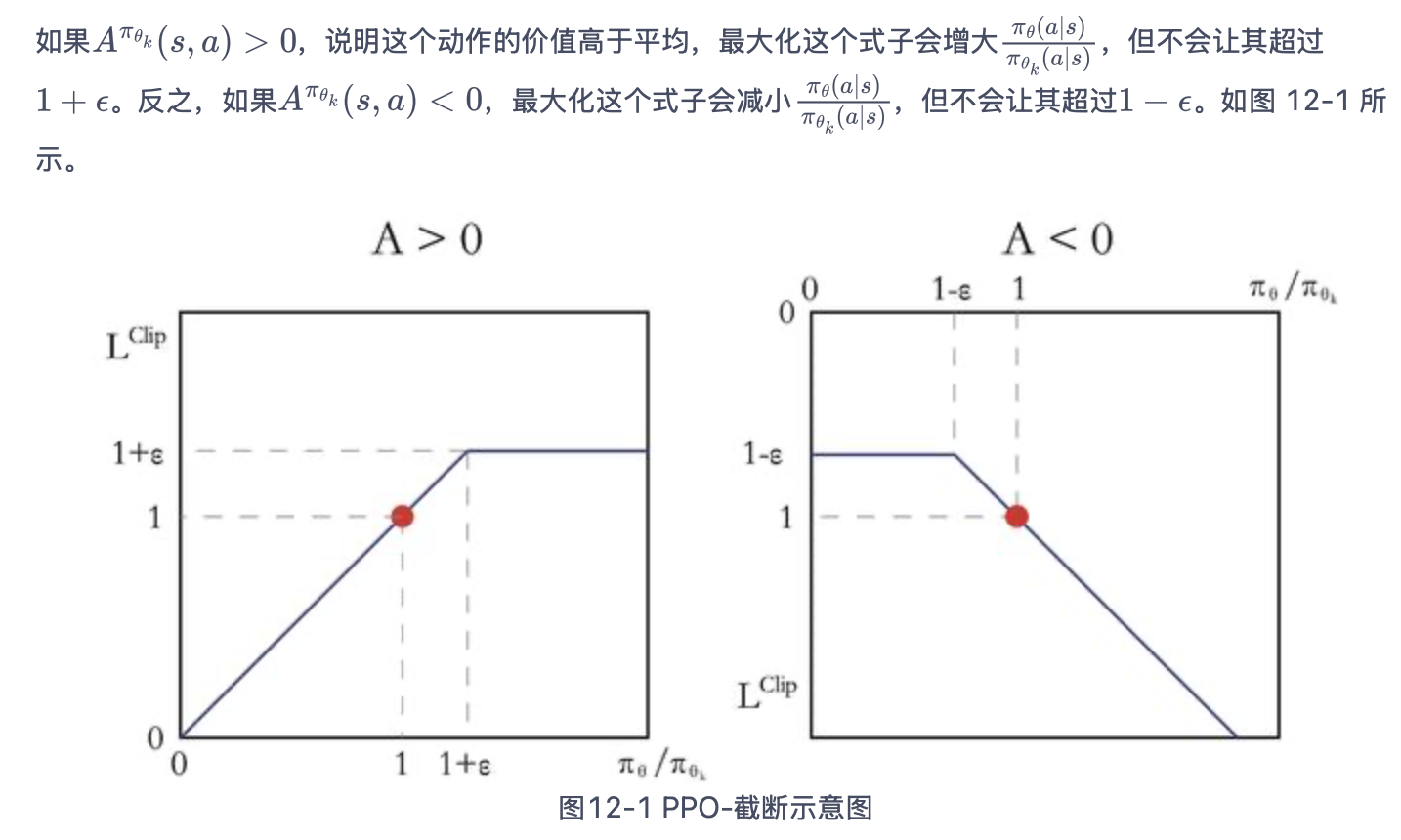
4. PPO-截断
在目标函数中进行限制,以保证新的参数和旧的参数的差距不会太大。

前一项是原来的,后一项是要做截断的;
保证更新幅度不会过大或过小。
5. PPO 代码实践
大量实验表明,PPO-截断总是比 PPO-惩罚表现得更好。因此下面我们使用 PPO-截断 的代码实现。

TD 误差
计算TD目标
td_target = rewards + γ * critic(next_states) * (1 - dones)rewards:当前获得的即时奖励(r_t)critic(next_states):critic网络对下一状态的估值(V(s_{t+1}))(1 - dones):终止状态处理(如果done=True,则忽略后续状态价值)
计算TD误差
td_delta = td_target - critic(states)critic(states):critic 网络对当前状态的估值(V(s_t))- 结果即为
δ_t = (r_t + γV(s_{t+1})) - V(s_t)

优势函数(GAE)
核心:对多个时间步的TD误差进行加权平均
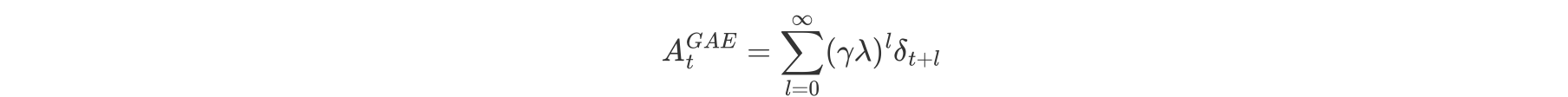
advantage = rl_utils.compute_advantage(gamma, lmbda, td_delta)
离散环境
定义策略网络和价值网络
import gym import torch import torch.nn.functional as F import numpy as np import matplotlib.pyplot as plt import rl_utils class PolicyNet(torch.nn.Module): def __init__(self, state_dim, hidden_dim, action_dim): super(PolicyNet, self).__init__() self.fc1 = torch.nn.Linear(state_dim, hidden_dim) self.fc2 = torch.nn.Linear(hidden_dim, action_dim) def forward(self, x): x = F.relu(self.fc1(x)) return F.softmax(self.fc2(x), dim=1) # 输出动作概率分布 class ValueNet(torch.nn.Module): def __init__(self, state_dim, hidden_dim): super(ValueNet, self).__init__() self.fc1 = torch.nn.Linear(state_dim, hidden_dim) self.fc2 = torch.nn.Linear(hidden_dim, 1) def forward(self, x): x = F.relu(self.fc1(x)) return self.fc2(x) # 不接激活函数,直接输出值 class PPO: ''' PPO算法,采用截断方式 ''' def __init__(self, state_dim, hidden_dim, action_dim, actor_lr, critic_lr, lmbda, epochs, eps, gamma, device): self.actor = PolicyNet(state_dim, hidden_dim, action_dim).to(device) self.critic = ValueNet(state_dim, hidden_dim).to(device) self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=actor_lr) self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=critic_lr) self.gamma = gamma # 折扣因子 self.lmbda = lmbda # GAE参数 self.epochs = epochs # 一条序列的数据用来训练轮数 self.eps = eps # PPO中截断范围的参数 self.device = device '''通过策略网络得到动作概率分布;使用分类分布进行动作采样''' def take_action(self, state): state = torch.tensor([state], dtype=torch.float).to(self.device) probs = self.actor(state) action_dist = torch.distributions.Categorical(probs) action = action_dist.sample() return action.item() '''关键部分,实现了PPO的更新逻辑。''' def update(self, transition_dict): states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device) actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(self.device) rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device) next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device) dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device) # 计算TD目标 td_target = rewards + self.gamma * self.critic(next_states) * (1 - dones) # 计算优势函数(使用GAE) td_delta = td_target - self.critic(states) advantage = rl_utils.compute_advantage(self.gamma, self.lmbda, td_delta.cpu()).to(self.device) # 旧策略的概率(固定不更新) old_log_probs = torch.log(self.actor(states).gather(1, actions)).detach() for _ in range(self.epochs): # 计算新旧策略概率比 log_probs = torch.log(self.actor(states).gather(1, actions)) ratio = torch.exp(log_probs - old_log_probs) # PPO核心损失计算 surr1 = ratio * advantage surr2 = torch.clamp(ratio, 1 - self.eps, 1 + self.eps) * advantage # 截断 actor_loss = torch.mean(-torch.min(surr1, surr2)) # PPO损失函数 # 价值网络损失 critic_loss = torch.mean(F.mse_loss(self.critic(states), td_target.detach())) # 反向传播更新 self.actor_optimizer.zero_grad() self.critic_optimizer.zero_grad() actor_loss.backward() critic_loss.backward() self.actor_optimizer.step() self.critic_optimizer.step()在车杆环境中训练 PPO 算法
actor_lr = 1e-3 critic_lr = 1e-2 num_episodes = 500 hidden_dim = 128 gamma = 0.98 lmbda = 0.95 epochs = 10 eps = 0.2 device = torch.device("cuda") if torch.cuda.is_available() else torch.device( "cpu") env_name = 'CartPole-v0' env = gym.make(env_name) env.seed(0) torch.manual_seed(0) state_dim = env.observation_space.shape[0] action_dim = env.action_space.n agent = PPO(state_dim, hidden_dim, action_dim, actor_lr, critic_lr, lmbda, epochs, eps, gamma, device) return_list = rl_utils.train_on_policy_agent(env, agent, num_episodes)
连续环境
让策略网络输出连续动作高斯分布的均值和标准差。后续的连续动作则在该高斯分布中采样得到。
定义网络
class PolicyNetContinuous(torch.nn.Module): def __init__(self, state_dim, hidden_dim, action_dim): super(PolicyNetContinuous, self).__init__() self.fc1 = torch.nn.Linear(state_dim, hidden_dim) self.fc_mu = torch.nn.Linear(hidden_dim, action_dim) self.fc_std = torch.nn.Linear(hidden_dim, action_dim) def forward(self, x): x = F.relu(self.fc1(x)) mu = 2.0 * torch.tanh(self.fc_mu(x)) std = F.softplus(self.fc_std(x)) return mu, std class PPOContinuous: ''' 处理连续动作的PPO算法 ''' def __init__(self, state_dim, hidden_dim, action_dim, actor_lr, critic_lr, lmbda, epochs, eps, gamma, device): self.actor = PolicyNetContinuous(state_dim, hidden_dim, action_dim).to(device) self.critic = ValueNet(state_dim, hidden_dim).to(device) self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=actor_lr) self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=critic_lr) self.gamma = gamma self.lmbda = lmbda self.epochs = epochs self.eps = eps self.device = device def take_action(self, state): state = torch.tensor([state], dtype=torch.float).to(self.device) mu, sigma = self.actor(state) action_dist = torch.distributions.Normal(mu, sigma) action = action_dist.sample() return [action.item()] def update(self, transition_dict): states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device) actions = torch.tensor(transition_dict['actions'], dtype=torch.float).view(-1, 1).to(self.device) rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device) next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device) dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device) rewards = (rewards + 8.0) / 8.0 # 和TRPO一样,对奖励进行修改,方便训练 td_target = rewards + self.gamma * self.critic(next_states) * (1 - dones) td_delta = td_target - self.critic(states) advantage = rl_utils.compute_advantage(self.gamma, self.lmbda, td_delta.cpu()).to(self.device) mu, std = self.actor(states) action_dists = torch.distributions.Normal(mu.detach(), std.detach()) # 动作是正态分布 old_log_probs = action_dists.log_prob(actions) for _ in range(self.epochs): mu, std = self.actor(states) action_dists = torch.distributions.Normal(mu, std) log_probs = action_dists.log_prob(actions) ratio = torch.exp(log_probs - old_log_probs) surr1 = ratio * advantage surr2 = torch.clamp(ratio, 1 - self.eps, 1 + self.eps) * advantage actor_loss = torch.mean(-torch.min(surr1, surr2)) critic_loss = torch.mean( F.mse_loss(self.critic(states), td_target.detach())) self.actor_optimizer.zero_grad() self.critic_optimizer.zero_grad() actor_loss.backward() critic_loss.backward() self.actor_optimizer.step() self.critic_optimizer.step()在倒立摆环境中训练
创建环境
Pendulum-v0,并设定随机数种子以便重复实现。actor_lr = 1e-4 critic_lr = 5e-3 num_episodes = 2000 hidden_dim = 128 gamma = 0.9 lmbda = 0.9 epochs = 10 eps = 0.2 device = torch.device("cuda") if torch.cuda.is_available() else torch.device( "cpu") env_name = 'Pendulum-v0' env = gym.make(env_name) env.seed(0) torch.manual_seed(0) state_dim = env.observation_space.shape[0] action_dim = env.action_space.shape[0] # 连续动作空间 agent = PPOContinuous(state_dim, hidden_dim, action_dim, actor_lr, critic_lr, lmbda, epochs, eps, gamma, device) return_list = rl_utils.train_on_policy_agent(env, agent, num_episodes)
6. PPO 在 ChatGPT 中的使用
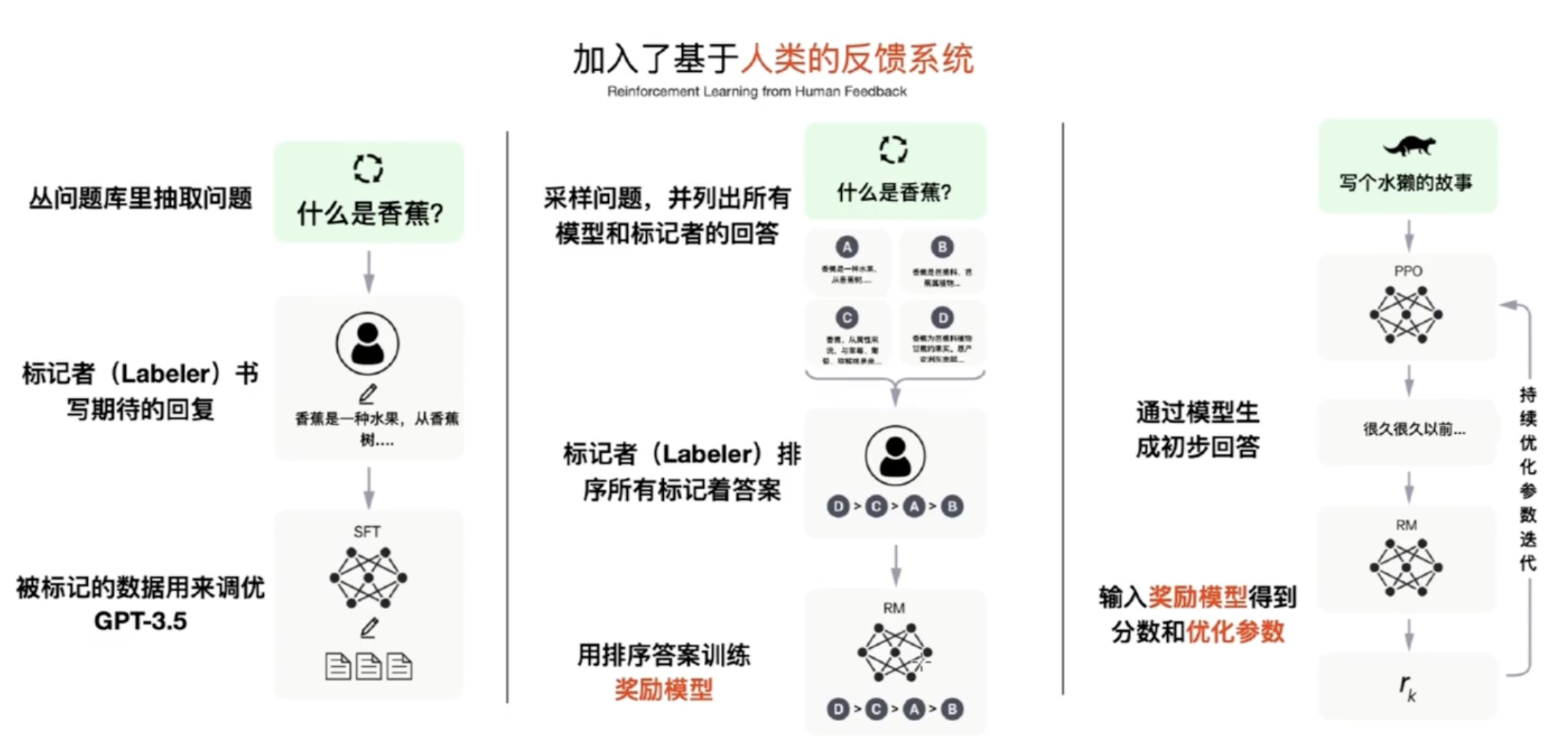
总结
PPO 是 TRPO 的一种改进算法,它在实现上简化了 TRPO 中的复杂计算,并且它在实验中的性能大多数情况下会比 TRPO 更好,因此目前常被用作一种常用的基准算法。
TRPO 和 PPO 都属于在线策略学习算法,即使优化目标中包含重要性采样的过程,但其只是用到了上一轮策略的数据,而不是过去所有策略的数据。