Q-learing
无模型的强化学习:不需要事先知道环境的奖励函数和状态转移函数,而是直接使用和环境交互的过程中采样到的数据来学习。
1. 时序差分方法
时序差分方法核心:对未来动作选择的价值估计来更新对当前动作选择的价值估计。
蒙特卡洛方法(Monte-Carlo methods)
使用重复随机抽样,然后运用概率统计方法来从抽样结果中归纳出我们想求的目标的数值估计。
用蒙特卡洛方法来估计一个策略在一个马尔可夫决策过程中的状态价值函数:用样本均值作为期望值的估计
- 在 MDP 上采样很多条序列,计算从这个状态出发的回报再求其期望
- 一条序列只计算一次回报,也就是这条序列第一次出现该状态时计算后面的累积奖励,而后面再次出现该状态时,该状态就被忽略了。
蒙特卡洛方法对价值函数的增量更新方式
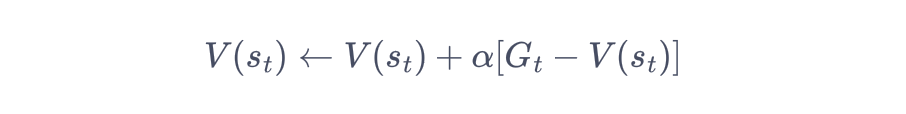
时序差分方法只需要当前步结束即可进行计算

时序差分误差(TD Error)
目标:衡量当前价值预测与更准确的目标估计之间的差异

2. Sarsa 算法:在线策略
在不知道奖励函数和状态转移函数的情况下该怎么进行策略提升呢?
直接用时序差分算法来估计动作价值函数 Q:
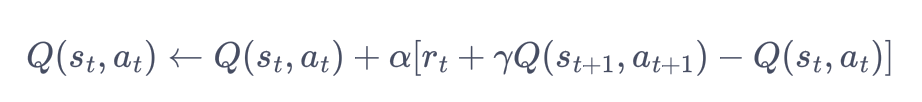
然后用贪婪算法来选取在某个状态下动作价值最大的那个动作,即 agrmaxQ(s,a)。
但是,不能一直是贪婪:

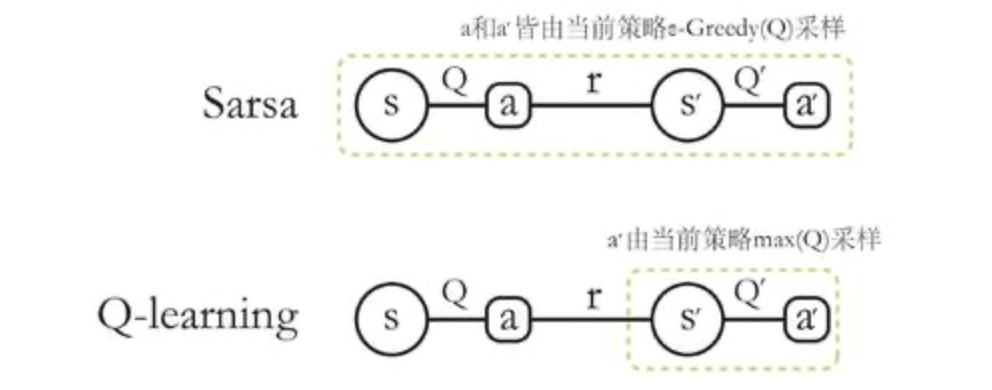
Sarsa

必须使用当前贪婪策略采样得到的数据
3. Q-learning:离线策略
Q-learning 的时序差分更新方式:

不一定必须使用当前贪心策略采样得到的数据,因为**给定任意(s, a, r, s’)**都可以直接根据更新公式来更新Q;为了探索,我们通常使用一个ε-贪婪策略来与环境交互。
class QLearning:
""" Q-learning算法 """
def __init__(self, ncol, nrow, epsilon, alpha, gamma, n_action=4):
self.Q_table = np.zeros([nrow * ncol, n_action]) # 初始化Q(s,a)表格
self.n_action = n_action # 动作个数
self.alpha = alpha # 学习率
self.gamma = gamma # 折扣因子
self.epsilon = epsilon # epsilon-贪婪策略中的参数
def take_action(self, state): #选取下一步的操作
if np.random.random() < self.epsilon:
action = np.random.randint(self.n_action)
else:
action = np.argmax(self.Q_table[state])
return action
def best_action(self, state): # 用于打印策略
Q_max = np.max(self.Q_table[state])
a = [0 for _ in range(self.n_action)]
for i in range(self.n_action):
if self.Q_table[state, i] == Q_max:
a[i] = 1
return a
def update(self, s0, a0, r, s1):
td_error = r + self.gamma * self.Q_table[s1].max(
) - self.Q_table[s0, a0]
self.Q_table[s0, a0] += self.alpha * td_error
np.random.seed(0)
epsilon = 0.1
alpha = 0.1
gamma = 0.9
agent = QLearning(ncol, nrow, epsilon, alpha, gamma)
num_episodes = 500 # 智能体在环境中运行的序列的数量
return_list = [] # 记录每一条序列的回报
for i in range(10): # 显示10个进度条
# tqdm的进度条功能
with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
for i_episode in range(int(num_episodes / 10)): # 每个进度条的序列数
episode_return = 0
state = env.reset()
done = False
while not done:
action = agent.take_action(state)
next_state, reward, done = env.step(action)
episode_return += reward # 这里回报的计算不进行折扣因子衰减
agent.update(state, action, reward, next_state)
state = next_state
return_list.append(episode_return)
if (i_episode + 1) % 10 == 0: # 每10条序列打印一下这10条序列的平均回报
pbar.set_postfix({
'episode':
'%d' % (num_episodes / 10 * i + i_episode + 1),
'return':
'%.3f' % np.mean(return_list[-10:])
})
pbar.update(1)
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('Q-learning on {}'.format('Cliff Walking'))
plt.show()
action_meaning = ['^', 'v', '<', '>']
print('Q-learning算法最终收敛得到的策略为:')
print_agent(agent, env, action_meaning, list(range(37, 47)), [47])