TRPO
基于策略的方法的缺点:当策略网络是深度模型时沿着策略梯度更新参数,很有可能由于步长太长,策略突然显著变差,进而影响训练效果。
信任区域策略优化(TRPO)算法的核心思想:
信任区域(trust region):在这个区域上更新策略时能够得到某种策略性能的安全性保证。
1. 策略目标


πθ’ 是我们需要求解的策略,但我们又要用它来收集样本,不现实。
TRPO 对状态访问分布进行处理:忽略两个策略之间的状态访问分布变化,直接采用旧的策略 πθ 的状态分布,定义如下替代优化目标:
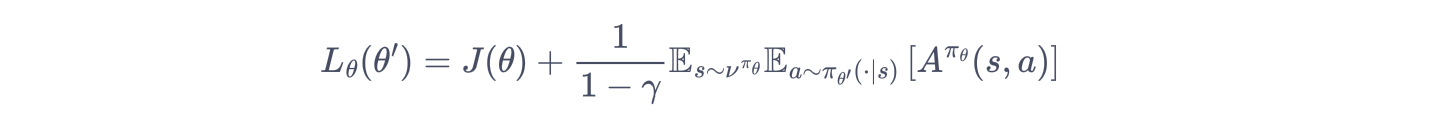
可以用重要性采样对动作分布进行处理:
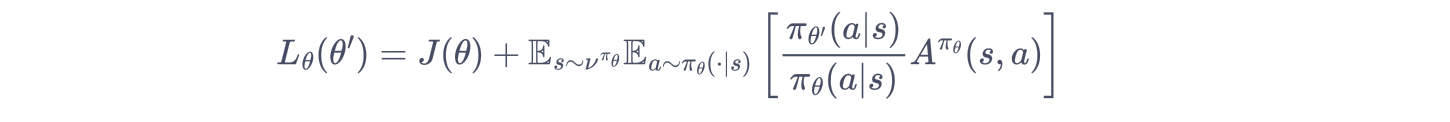
这样,就可以基于旧策略已经采样出的数据来估计并优化新策略了。
2. 库尔贝克-莱布勒(Kullback-Leibler,KL)散度
整体优化公式如下:
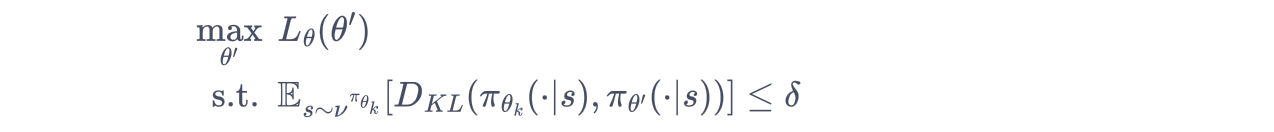
其中 KL散度 用于衡量策略之间的距离。:

该不等式约束定义了策略空间中的一个 KL 球,被称为信任区域。
在这个区域中,可认为当前学习策略和环境交互的状态分布与上一轮策略最后采样的状态分布一致,进而可以基于一步行动的重要性采样方法使当前学习策略稳定提升。
3. 近似求解
求解上式带约束的优化问题 —— 用近似操作快速求解。
通过泰勒展开,将优化目标变成:
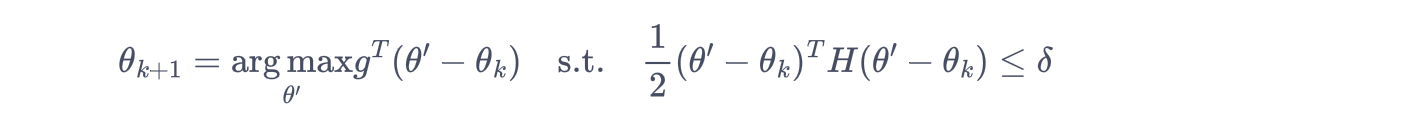

黑塞矩阵(Hessian Matrix)
黑塞矩阵是一个多元函数的二阶偏导数构成的对称方阵,用于描述函数在某点的局部曲率。
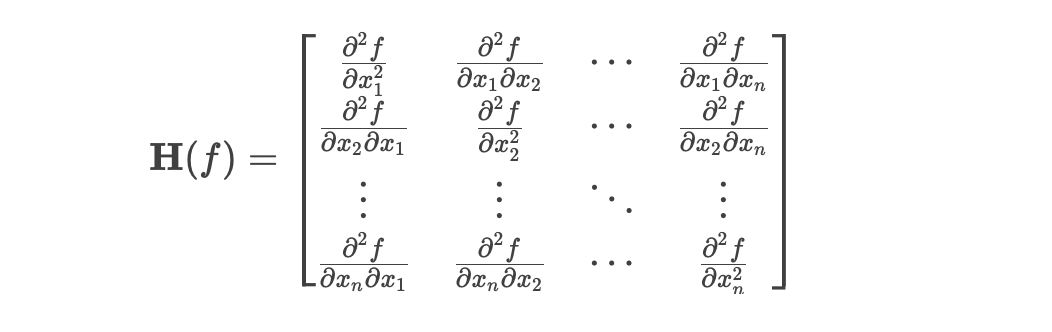

KKT条件
非线性优化问题(特别是约束优化问题)中判定最优解的必要条件


4. 共轭梯度
目的:
TRPO 通过共轭梯度法(conjugate gradient method)节约参数的内存资源和时间。
核心思想:直接计算 x = H-1g (x是参数更新方向)
具体流程:

(为什么强化学习有那么多数学?我要看晕了 我想去吃饭了…最后两个概念 加油!!!
5. 线性搜索(Line Search)
目的:
之前用 1 阶和 2 阶近似,并非精确求解。故 TRPO 每次迭代进行一次 线性搜索,找到一个最小的非负整数 i,使按照

具体流程:

6. 广义优势估计(Generalized Advantage Estimation,GAE)
目的:
通过指数加权平均不同步长的优势估计(从1步到无穷步),求解优势函数 A。


γ 折扣因子:决定未来奖励的权重。
λ GAE参数:控制优势估计中不同步长回报的权衡。
δt 时序差分误差:反映当前状态值函数的估计质量。
- 若 δt>0,说明实际回报高于预期,动作可能更优;若 δt<0,则相反。
给定 γ,λ 和每个时间步后的 δt,即可直接公式求解优势估计。
GAE 实现代码:

def compute_advantage(gamma, lmbda, td_delta): td_delta = td_delta.detach().numpy() advantage_list = [] advantage = 0.0 for delta in td_delta[::-1]: advantage = delta + gamma * lmbda * advantage advantage_list.append(advantage) advantage_list.reverse() return torch.tensor(advantage_list, dtype=torch.float)
7. TRPO 代码实践
import torch
import numpy as np
import gym
import matplotlib.pyplot as plt
import torch.nn.functional as F
import rl_utils
import copy
离散环境
定义策略网络和价值网络
class PolicyNet(torch.nn.Module): def __init__(self, state_dim, hidden_dim, action_dim): super(PolicyNet, self).__init__() self.fc1 = torch.nn.Linear(state_dim, hidden_dim) self.fc2 = torch.nn.Linear(hidden_dim, action_dim) def forward(self, x): x = F.relu(self.fc1(x)) return F.softmax(self.fc2(x), dim=1) class ValueNet(torch.nn.Module): def __init__(self, state_dim, hidden_dim): super(ValueNet, self).__init__() self.fc1 = torch.nn.Linear(state_dim, hidden_dim) self.fc2 = torch.nn.Linear(hidden_dim, 1) def forward(self, x): x = F.relu(self.fc1(x)) return self.fc2(x) class TRPO: """ TRPO算法 """ def __init__(self, hidden_dim, state_space, action_space, lmbda, kl_constraint, alpha, critic_lr, gamma, device): state_dim = state_space.shape[0] action_dim = action_space.n # 策略网络参数不需要优化器更新 self.actor = PolicyNet(state_dim, hidden_dim, action_dim).to(device) self.critic = ValueNet(state_dim, hidden_dim).to(device) self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=critic_lr) self.gamma = gamma self.lmbda = lmbda # GAE参数 self.kl_constraint = kl_constraint # KL距离最大限制 self.alpha = alpha # 线性搜索参数 self.device = device def take_action(self, state): state = torch.tensor([state], dtype=torch.float).to(self.device) probs = self.actor(state) action_dist = torch.distributions.Categorical(probs) action = action_dist.sample() return action.item() def hessian_matrix_vector_product(self, states, old_action_dists, vector): # 计算黑塞矩阵和一个向量的乘积 new_action_dists = torch.distributions.Categorical(self.actor(states)) kl = torch.mean( torch.distributions.kl.kl_divergence(old_action_dists, new_action_dists)) # 计算平均KL距离 kl_grad = torch.autograd.grad(kl, self.actor.parameters(), create_graph=True) kl_grad_vector = torch.cat([grad.view(-1) for grad in kl_grad]) # KL距离的梯度先和向量进行点积运算 kl_grad_vector_product = torch.dot(kl_grad_vector, vector) grad2 = torch.autograd.grad(kl_grad_vector_product, self.actor.parameters()) grad2_vector = torch.cat([grad.view(-1) for grad in grad2]) return grad2_vector def conjugate_gradient(self, grad, states, old_action_dists): # 共轭梯度法求解方程 x = torch.zeros_like(grad) r = grad.clone() p = grad.clone() rdotr = torch.dot(r, r) for i in range(10): # 共轭梯度主循环 Hp = self.hessian_matrix_vector_product(states, old_action_dists, p) alpha = rdotr / torch.dot(p, Hp) x += alpha * p r -= alpha * Hp new_rdotr = torch.dot(r, r) if new_rdotr < 1e-10: break beta = new_rdotr / rdotr p = r + beta * p rdotr = new_rdotr return x def compute_surrogate_obj(self, states, actions, advantage, old_log_probs, actor): # 计算策略目标 log_probs = torch.log(actor(states).gather(1, actions)) ratio = torch.exp(log_probs - old_log_probs) return torch.mean(ratio * advantage) def line_search(self, states, actions, advantage, old_log_probs, old_action_dists, max_vec): # 线性搜索 old_para = torch.nn.utils.convert_parameters.parameters_to_vector( self.actor.parameters()) old_obj = self.compute_surrogate_obj(states, actions, advantage, old_log_probs, self.actor) for i in range(15): # 线性搜索主循环 coef = self.alpha**i new_para = old_para + coef * max_vec new_actor = copy.deepcopy(self.actor) torch.nn.utils.convert_parameters.vector_to_parameters( new_para, new_actor.parameters()) new_action_dists = torch.distributions.Categorical( new_actor(states)) kl_div = torch.mean( torch.distributions.kl.kl_divergence(old_action_dists, new_action_dists)) new_obj = self.compute_surrogate_obj(states, actions, advantage, old_log_probs, new_actor) if new_obj > old_obj and kl_div < self.kl_constraint: return new_para return old_para def policy_learn(self, states, actions, old_action_dists, old_log_probs, advantage): # 更新策略函数 surrogate_obj = self.compute_surrogate_obj(states, actions, advantage, old_log_probs, self.actor) grads = torch.autograd.grad(surrogate_obj, self.actor.parameters()) obj_grad = torch.cat([grad.view(-1) for grad in grads]).detach() # 用共轭梯度法计算x = H^(-1)g descent_direction = self.conjugate_gradient(obj_grad, states, old_action_dists) Hd = self.hessian_matrix_vector_product(states, old_action_dists, descent_direction) max_coef = torch.sqrt(2 * self.kl_constraint / (torch.dot(descent_direction, Hd) + 1e-8)) new_para = self.line_search(states, actions, advantage, old_log_probs, old_action_dists, descent_direction * max_coef) # 线性搜索 torch.nn.utils.convert_parameters.vector_to_parameters( new_para, self.actor.parameters()) # 用线性搜索后的参数更新策略 def update(self, transition_dict): states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device) actions = torch.tensor(transition_dict['actions']).view(-1, 1).to( self.device) rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device) next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device) dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device) td_target = rewards + self.gamma * self.critic(next_states) * (1 - dones) td_delta = td_target - self.critic(states) advantage = compute_advantage(self.gamma, self.lmbda, td_delta.cpu()).to(self.device) old_log_probs = torch.log(self.actor(states).gather(1, actions)).detach() old_action_dists = torch.distributions.Categorical( self.actor(states).detach()) critic_loss = torch.mean( F.mse_loss(self.critic(states), td_target.detach())) self.critic_optimizer.zero_grad() critic_loss.backward() self.critic_optimizer.step() # 更新价值函数 # 更新策略函数 self.policy_learn(states, actions, old_action_dists, old_log_probs, advantage)在车杆环境中训练 TRPO
num_episodes = 500 hidden_dim = 128 gamma = 0.98 lmbda = 0.95 critic_lr = 1e-2 kl_constraint = 0.0005 alpha = 0.5 device = torch.device("cuda") if torch.cuda.is_available() else torch.device( "cpu") env_name = 'CartPole-v0' env = gym.make(env_name) env.seed(0) torch.manual_seed(0) agent = TRPO(hidden_dim, env.observation_space, env.action_space, lmbda, kl_constraint, alpha, critic_lr, gamma, device) return_list = rl_utils.train_on_policy_agent(env, agent, num_episodes) episodes_list = list(range(len(return_list))) plt.plot(episodes_list, return_list) plt.xlabel('Episodes') plt.ylabel('Returns') plt.title('TRPO on {}'.format(env_name)) plt.show() mv_return = rl_utils.moving_average(return_list, 9) plt.plot(episodes_list, mv_return) plt.xlabel('Episodes') plt.ylabel('Returns') plt.title('TRPO on {}'.format(env_name)) plt.show()
连续环境
对于策略网络,因为环境是连续动作的,所以策略网络分别输出表示动作分布的高斯分布的均值和标准差。
class PolicyNetContinuous(torch.nn.Module):
def __init__(self, state_dim, hidden_dim, action_dim):
super(PolicyNetContinuous, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc_mu = torch.nn.Linear(hidden_dim, action_dim)
self.fc_std = torch.nn.Linear(hidden_dim, action_dim)
def forward(self, x):
x = F.relu(self.fc1(x))
mu = 2.0 * torch.tanh(self.fc_mu(x))
std = F.softplus(self.fc_std(x))
return mu, std # 高斯分布的均值和标准差
class TRPOContinuous:
""" 处理连续动作的TRPO算法 """
def __init__(self, hidden_dim, state_space, action_space, lmbda,
kl_constraint, alpha, critic_lr, gamma, device):
state_dim = state_space.shape[0]
action_dim = action_space.shape[0]
self.actor = PolicyNetContinuous(state_dim, hidden_dim,
action_dim).to(device)
self.critic = ValueNet(state_dim, hidden_dim).to(device)
self.critic_optimizer = torch.optim.Adam(self.critic.parameters(),
lr=critic_lr)
self.gamma = gamma
self.lmbda = lmbda
self.kl_constraint = kl_constraint
self.alpha = alpha
self.device = device
def take_action(self, state):
state = torch.tensor([state], dtype=torch.float).to(self.device)
mu, std = self.actor(state)
action_dist = torch.distributions.Normal(mu, std)
action = action_dist.sample()
return [action.item()]
def hessian_matrix_vector_product(self,
states,
old_action_dists,
vector,
damping=0.1):
mu, std = self.actor(states)
new_action_dists = torch.distributions.Normal(mu, std)
kl = torch.mean(
torch.distributions.kl.kl_divergence(old_action_dists,
new_action_dists))
kl_grad = torch.autograd.grad(kl,
self.actor.parameters(),
create_graph=True)
kl_grad_vector = torch.cat([grad.view(-1) for grad in kl_grad])
kl_grad_vector_product = torch.dot(kl_grad_vector, vector)
grad2 = torch.autograd.grad(kl_grad_vector_product,
self.actor.parameters())
grad2_vector = torch.cat(
[grad.contiguous().view(-1) for grad in grad2])
return grad2_vector + damping * vector
def conjugate_gradient(self, grad, states, old_action_dists):
x = torch.zeros_like(grad)
r = grad.clone()
p = grad.clone()
rdotr = torch.dot(r, r)
for i in range(10):
Hp = self.hessian_matrix_vector_product(states, old_action_dists,
p)
alpha = rdotr / torch.dot(p, Hp)
x += alpha * p
r -= alpha * Hp
new_rdotr = torch.dot(r, r)
if new_rdotr < 1e-10:
break
beta = new_rdotr / rdotr
p = r + beta * p
rdotr = new_rdotr
return x
def compute_surrogate_obj(self, states, actions, advantage, old_log_probs,
actor):
mu, std = actor(states)
action_dists = torch.distributions.Normal(mu, std)
log_probs = action_dists.log_prob(actions)
ratio = torch.exp(log_probs - old_log_probs)
return torch.mean(ratio * advantage)
def line_search(self, states, actions, advantage, old_log_probs,
old_action_dists, max_vec):
old_para = torch.nn.utils.convert_parameters.parameters_to_vector(
self.actor.parameters())
old_obj = self.compute_surrogate_obj(states, actions, advantage,
old_log_probs, self.actor)
for i in range(15):
coef = self.alpha**i
new_para = old_para + coef * max_vec
new_actor = copy.deepcopy(self.actor)
torch.nn.utils.convert_parameters.vector_to_parameters(
new_para, new_actor.parameters())
mu, std = new_actor(states)
new_action_dists = torch.distributions.Normal(mu, std)
kl_div = torch.mean(
torch.distributions.kl.kl_divergence(old_action_dists,
new_action_dists))
new_obj = self.compute_surrogate_obj(states, actions, advantage,
old_log_probs, new_actor)
if new_obj > old_obj and kl_div < self.kl_constraint:
return new_para
return old_para
def policy_learn(self, states, actions, old_action_dists, old_log_probs,
advantage):
surrogate_obj = self.compute_surrogate_obj(states, actions, advantage,
old_log_probs, self.actor)
grads = torch.autograd.grad(surrogate_obj, self.actor.parameters())
obj_grad = torch.cat([grad.view(-1) for grad in grads]).detach()
descent_direction = self.conjugate_gradient(obj_grad, states,
old_action_dists)
Hd = self.hessian_matrix_vector_product(states, old_action_dists,
descent_direction)
max_coef = torch.sqrt(2 * self.kl_constraint /
(torch.dot(descent_direction, Hd) + 1e-8))
new_para = self.line_search(states, actions, advantage, old_log_probs,
old_action_dists,
descent_direction * max_coef)
torch.nn.utils.convert_parameters.vector_to_parameters(
new_para, self.actor.parameters())
def update(self, transition_dict):
states = torch.tensor(transition_dict['states'],
dtype=torch.float).to(self.device)
actions = torch.tensor(transition_dict['actions'],
dtype=torch.float).view(-1, 1).to(self.device)
rewards = torch.tensor(transition_dict['rewards'],
dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition_dict['next_states'],
dtype=torch.float).to(self.device)
dones = torch.tensor(transition_dict['dones'],
dtype=torch.float).view(-1, 1).to(self.device)
rewards = (rewards + 8.0) / 8.0 # 对奖励进行修改,方便训练
td_target = rewards + self.gamma * self.critic(next_states) * (1 -
dones)
td_delta = td_target - self.critic(states)
advantage = compute_advantage(self.gamma, self.lmbda,
td_delta.cpu()).to(self.device)
mu, std = self.actor(states)
old_action_dists = torch.distributions.Normal(mu.detach(),
std.detach())
old_log_probs = old_action_dists.log_prob(actions)
critic_loss = torch.mean(
F.mse_loss(self.critic(states), td_target.detach()))
self.critic_optimizer.zero_grad()
critic_loss.backward()
self.critic_optimizer.step()
self.policy_learn(states, actions, old_action_dists, old_log_probs,
advantage)
TRPO 算法属于在线策略:每次策略训练仅使用上一轮策略采样的数据。