Below you will find pages that utilize the taxonomy term “Algorithm”
「算法模版」动态规划
「状态」-> 「选择」 -> 定义 dp 数组/函数的含义 ;自底向上进行递推求解。
# 自顶向下递归的动态规划
def dp(状态1, 状态2, ...):
for 选择 in 所有可能的选择:
# 此时的状态已经因为做了选择而改变
result = 求最值(result, dp(状态1, 状态2, ...))
return result
# 自底向上迭代的动态规划
# 初始化 base case
dp[0][0][...] = base case
# 进行状态转移
for 状态1 in 状态1的所有取值:
for 状态2 in 状态2的所有取值:
for ...
dp[状态1][状态2][...] = 求最值(选择1,选择2...)
核心框架
备忘录 - 斐波那契数
int fib(int n) { if (n == 0 || n == 1) return n; // 分别代表 dp[i - 1] 和 dp[i - 2] int dp_i_1 = 1, dp_i_2 = 0; for (int i = 2; i <= n; i++) { int dp_i = dp_i_1 + dp_i_2; dp_i_2 = dp_i_1; dp_i_1 = dp_i; } return dp_i; }最优子结构 - 零点兑换
c++语法
万能开头:
#include<bits/stdc++.h>
using namespace std;
在 C++ 中,using namespace std;指令允许用户使用 std 命名空间中的所有标识符,而无需在它们前面加上 std::。
标准输入输出
标准输入是 cin, cin用 >> 运算符把输入传给变量。
标准输出是 cout,用 << 运算符把需要打印的内容传递给 cout,endl 是换行符。
#include <bits/stdc++.h>
int a;
cin >> a; // 从输入读取一个整数
// 输出a
std::cout << a << std::endl;
// 可以串联输出
// 输出:Hello, World!
std::cout << "Hello" << ", " << "World!" << std::endl;
string s = "abc";
a = 10;
// 输出:abc 10
std::cout << s << " " << a << std::endl;
算法 - C++STL常用容器
插入函数总结
| 方法 | 适用容器 | 作用 | 性能特性 |
|---|---|---|---|
push | queue、stack、priority_queue | 添加元素到容器末尾或顶部 | 适用于特定容器,性能与容器实现相关 |
push_back | vector、deque、list | 添加元素到容器末尾 | 需要拷贝或移动元素 |
emplace | set、map、unordered_set 等 | 在容器中直接构造元素 | 避免不必要的拷贝或移动 |
emplace_back | vector、deque、list | 在容器末尾直接构造元素 | 避免不必要的拷贝或移动 |
insert | 大多数容器 | 将元素插入到容器的指定位置 | 需要拷贝或移动元素 |
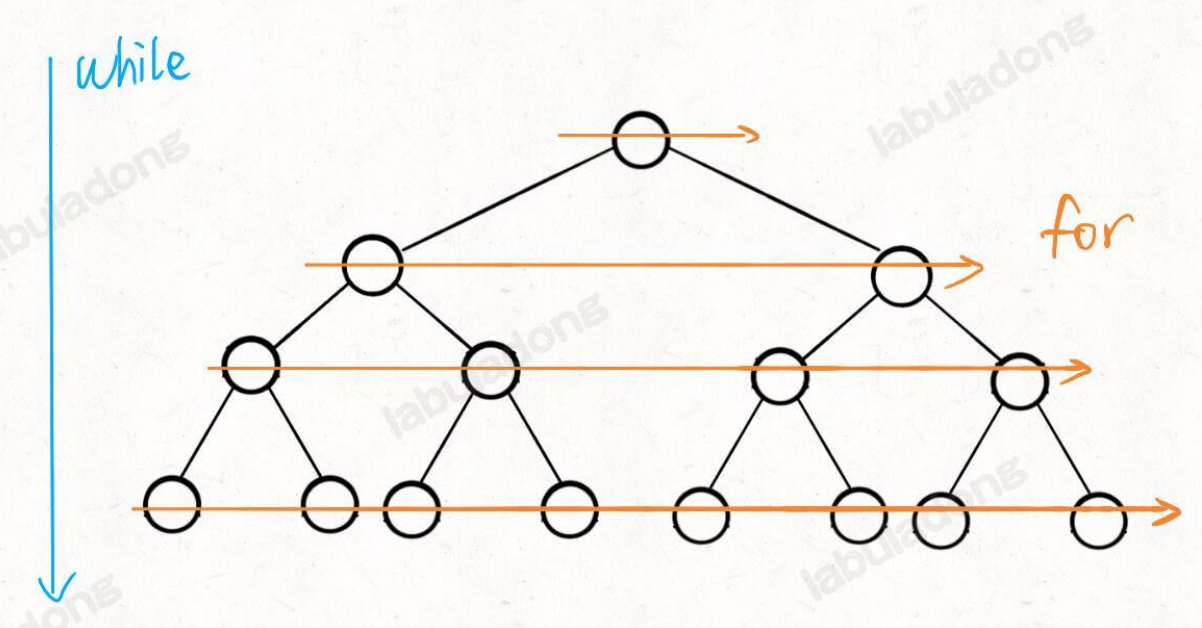
「算法模版」树
层级遍历
while 循环控制⼀层⼀层往下⾛,for 循环利⽤ sz 变量控制从左到右遍历每⼀层⼆叉树节点。
// 输⼊⼀棵⼆叉树的根节点,层序遍历这棵⼆叉树
void levelTraverse(TreeNode root) {
if (root == null) return 0;
Queue<TreeNode> q = new LinkedList<>();
q.push(root);
int depth = 1;
// 从上到下遍历⼆叉树的每⼀层
while (!q.isEmpty()) {
int sz = q.size();
// 从左到右遍历每⼀层的每个节点
for (int i = 0; i < sz; i++) {
TreeNode cur = q.poll();
printf("节点 %s 在第 %s 层", cur, depth);
// 将下⼀层节点放⼊队列
if (cur.left != null) {
q.push(cur.left);
}
if (cur.right != null) {
q.offer(cur.right);
}
}
depth++;
}
}
「算法模版」图
存储图
邻接矩阵
邻接表
// 对于每个点k,开一个单链表,存储k所有可以走到的点 // h[k]存储这个单链表的头结点 int h[N], e[N], ne[N], idx; // 添加一条边a->b void add(int a, int b) { e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ; } // 初始化 idx = 0; memset(h, -1, sizeof h);
回溯算法
回溯法:一种通过探索所有可能的候选解来找出所有的解的算法。如果候选解被确认不是一个解(或者至少不是最后一个解),回溯算法会通过在上一步进行一些变化抛弃该解,即回溯并且再次尝试。
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择 : 本层集合中的元素) {
处理节点;
backtracking(路径, 选择列表); // 递归
撤销处理; // 回溯
}
}
「持续更新」算法题笔记
万能开头
#include<bits/stdc++.h>
using namespace std;
在 C++ 中,using namespace std;指令允许用户使用 std 命名空间中的所有标识符,而无需在它们前面加上 std::。
leetcode hot 100
hash
两数之和
题目描述:给定一个整数数组
nums和一个整数目标值target,请你在该数组中找出 和为目标值target的那 两个 整数,并返回它们的数组下标。方法:找数
x,寻找数组中是否存在target - x。使用哈希表,可以将寻找
target - x的时间复杂度降低到从 O(N) 降低到 O(1) —— 创建一个哈希表,对于每一个x,我们首先查询哈希表中是否存在target - x,然后将x插入到哈希表中,即可保证不会让x和自己匹配。
二叉树
二叉树
二叉树的实现方式
最常见的二叉树就是类似链表那样的链式存储结构,每个二叉树节点有指向左右子节点的指针
class TreeNode { public: int val; TreeNode* left; TreeNode* right; // 构造函数,参数是int x, :后面的部分是初始化列表,{} 是构造函数的函数体为空,即不需要额外的操作。 TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} }; // 你可以这样构建一棵二叉树: TreeNode* root = new TreeNode(1); root->left = new TreeNode(2); root->right = new TreeNode(3); root->left->left = new TreeNode(4); root->right->left = new TreeNode(5); root->right->right = new TreeNode(6); // 构建出来的二叉树是这样的: // 1 // / \ // 2 3 // / / \ // 4 5 6public用法总结:public关键字用于指定类成员的访问权限,允许外部代码直接访问这些成员。- 如果不加
public,这些成员默认是private的,外部代码无法直接访问它们。
在
TreeNode的构造函数中,初始化列表的作用是:
数组链表
1. 动态数组
动态数组底层还是静态数组,只是自动帮我们进行数组空间的扩缩容,并把增删查改操作进行了封装。
// 创建动态数组
// 不用显式指定数组大小,它会根据实际存储的元素数量自动扩缩容
ArrayList<Integer> arr = new ArrayList<>();
for (int i = 0; i < 10; i++) {
// 在末尾追加元素,时间复杂度 O(1)
arr.add(i);
}
// 在中间插入元素,时间复杂度 O(N)
// 在索引 2 的位置插入元素 666
arr.add(2, 666);
// 在头部插入元素,时间复杂度 O(N)
arr.add(0, -1);
// 删除末尾元素,时间复杂度 O(1)
arr.remove(arr.size() - 1);
// 删除中间元素,时间复杂度 O(N)
// 删除索引 2 的元素
arr.remove(2);
// 根据索引查询元素,时间复杂度 O(1)
int a = arr.get(0);
// 根据索引修改元素,时间复杂度 O(1)
arr.set(0, 100);
// 根据元素值查找索引,时间复杂度 O(N)
int index = arr.indexOf(666);