Below you will find pages that utilize the taxonomy term “RL”
工具链-Carla
官方文档:https://carla.readthedocs.io/en/0.9.9/#getting-started
Carla是一款开源的 自动驾驶 仿真器,它基本可以用来帮助训练自动驾驶的所有模块,包括感知系统,Localization,规划系统等等。许多自动驾驶公司在进行实际路跑前都要在这Carla上先进行训练。
1. 基本架构
Client-Server 的交互形式
Carla主要分为Server与Client两个模块
强化学习-发展趋势
1阶段
RL:一种解决马尔可夫决策过程的方法。
分类:value-based算法(DQN)和 policy-based算法(PPO)。
应用方向:多智能体强化学习, 安全强化学习等等。
2 阶段
强化学习应用的论文描述严格(必须有以下内容):
- 非常准确的状态空间和动作空间定义
- 必须存在状态转移函数,不允许单步决策,也就是一个动作就gameover
- 必须有过程奖励,且需要存在牺牲短期的过程奖励而获取最大累计回报的case案例
应用方向:游戏AI(份额不大)
3 阶段
RL 落地的真正难点在于问题的真实构建,而非近似构建或策略求解等等方面的问题。从原先任务只有求解策略的过程是强化学习,变成了 构建问题+求解策略 统称为强化学习。
典型如 offline model-based RL 和 RLHF,其中核心的模块变成了通过神经网络模拟状态转移函数和奖励函数,策略求解反而在方法论中被一句带过。
这个过程可以被解耦,变成跟强化学习毫无相关的名词概念,例如世界模型概念等。对于RL,没有有效的交互环境下的就没法达到目标,有这种有效交互环境的实际应用场景却非常少。
工具链-强化学习
1. gym
官方文档:https://www.gymlibrary.dev
最小例子
CartPole-v0import gymenv = gym.make('CartPole-v0') env.reset() for _ in range(1000): env.render() env.step(env.action_space.sample()) # take a random action
观测 (Observations)
在 Gym 仿真中,每一次回合开始,需要先执行 reset() 函数,返回初始观测信息,然后根据标志位 done 的状态,来决定是否进行下一次回合。代码表示:
env.step() 函数对每一步进行仿真,返回 4 个参数:
观测 Observation (Object):当前 step 执行后,环境的观测(类型为对象)。例如,从相机获取的像素点,机器人各个关节的角度或棋盘游戏当前的状态等;
奖励 Reward (Float): 执行上一步动作(action)后,智体(agent)获得的奖励,不同的环境中奖励值变化范围也不相同,但是强化学习的目标就是使得总奖励值最大;
完成 Done (Boolen): 表示是否需要将环境重置
env.reset。
PPO
1. 论文详读
Proximal Policy Optimization Algorithms(Proximal:近似)
2. PPO
回顾 TRPO
使用 KL 散度约束 policy 的更新幅度;使用重要性采样
缺点:近似会带来误差(重要性采样的通病);解带约束的优化问题困难
PPO 的改进
TRPO 采用重要性采样 —-> PPO 采用 clip 截断,限制新旧策略差异,避免更新过大。
优势函数 At 选用多步时序差分
自适应的 KL 惩罚项
Critic网络训练:
通过最小化
critic_loss = MSE(critic(states), td_target),让critic的价值估计更准确Actor网络更新:
- TD误差的广义形式(GAE)被用作优势函数,指导策略更新方向
- 优势函数越大,表示该动作比平均表现更好,应被加强
3. PPO-惩罚
PPO-惩罚(PPO-Penalty):用拉格朗日乘数法将 KL 散度的限制放进了目标函数中,使其变成了一个无约束的优化问题,在迭代的过程中不断更新 KL 散度前的系数 beta。
Actor-Critic
Actor-Critic 算法本质上是基于策略的算法,因为这一系列算法的目标都是优化一个带参数的策略,只是会额外学习价值函数,从而帮助策略函数更好地学习。
Actor-Critic 算法则可以在每一步之后都进行更新,并且不对任务的步数做限制。
更一般形式的策略梯度

1. Actor(策略网络)
Actor 要做的是与环境交互,并在 Critic 价值函数的指导下用策略梯度学习一个更好的策略。
Actor 的更新采用策略梯度的原则。
2. Critic(价值网络)
Critic 要做的是通过 Actor 与环境交互收集的数据学习一个价值函数,这个价值函数会用于判断在当前状态什么动作是好的,什么动作不是好的,进而帮助 Actor 进行策略更新。
REINFORCE
Q-learning、DQN 算法都是基于价值(value-based)的方法
- Q-learning 是处理有限状态的算法
- DQN 可以用来解决连续状态的问题
在强化学习中,除了基于值函数的方法,还有一支非常经典的方法,那就是基于策略(policy-based)的方法。
对比 value-based 和 policy-based
- 基于值函数:主要是学习值函数,然后根据值函数导出一个策略,学习过程中并不存在一个显式的策略;
- 基于策略:直接显式地学习一个目标策略。策略梯度是基于策略的方法的基础。
1. 策略梯度
将策略参数化:寻找一个最优策略并最大化这个策略在环境中的期望回报,即调整策略参数使平均回报最大化。
策略学习的目标函数

- J(θ) 是策略的目标函数(想要最大化的量);
- πθ 是参数为θ的随机性策略,并且处处可微(可以理解为AI的决策规则);
- Vπθ(s0) 指从初始状态s₀开始遵循策略π能获得的预期总回报;
- Es0 是对所有可能的初始状态求期望。
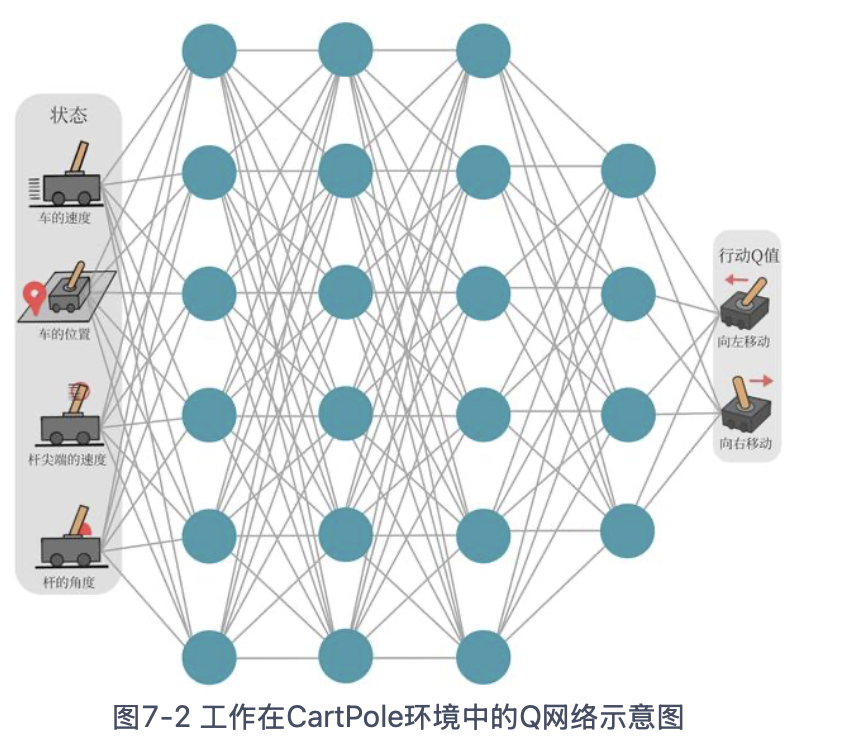
DQN (deep Q network)
Q-learning 算法用表格存储动作价值的做法只在 环境的状态和动作都是离散的,并且空间都比较小 的情况下适用.
DQN:用来解决连续状态下离散动作的问题,是离线策略算法,可以使用ε-贪婪策略来平衡探索与利用。
Q 网络:用于拟合函数Q函数的神经网络
Q 网络的损失函数(均方误差形式)
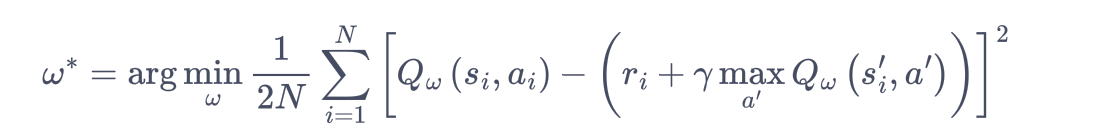
Q-learing
无模型的强化学习:不需要事先知道环境的奖励函数和状态转移函数,而是直接使用和环境交互的过程中采样到的数据来学习。
1. 时序差分方法
时序差分方法核心:对未来动作选择的价值估计来更新对当前动作选择的价值估计。
蒙特卡洛方法(Monte-Carlo methods)
使用重复随机抽样,然后运用概率统计方法来从抽样结果中归纳出我们想求的目标的数值估计。
用蒙特卡洛方法来估计一个策略在一个马尔可夫决策过程中的状态价值函数:用样本均值作为期望值的估计
- 在 MDP 上采样很多条序列,计算从这个状态出发的回报再求其期望
- 一条序列只计算一次回报,也就是这条序列第一次出现该状态时计算后面的累积奖励,而后面再次出现该状态时,该状态就被忽略了。
蒙特卡洛方法对价值函数的增量更新方式
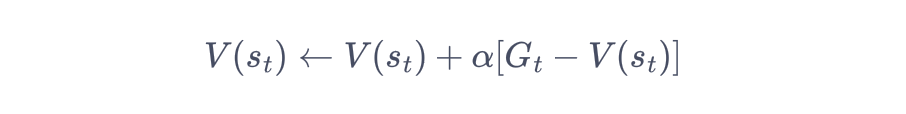
时序差分方法只需要当前步结束即可进行计算
PPO-直观理解
1. 基础概念
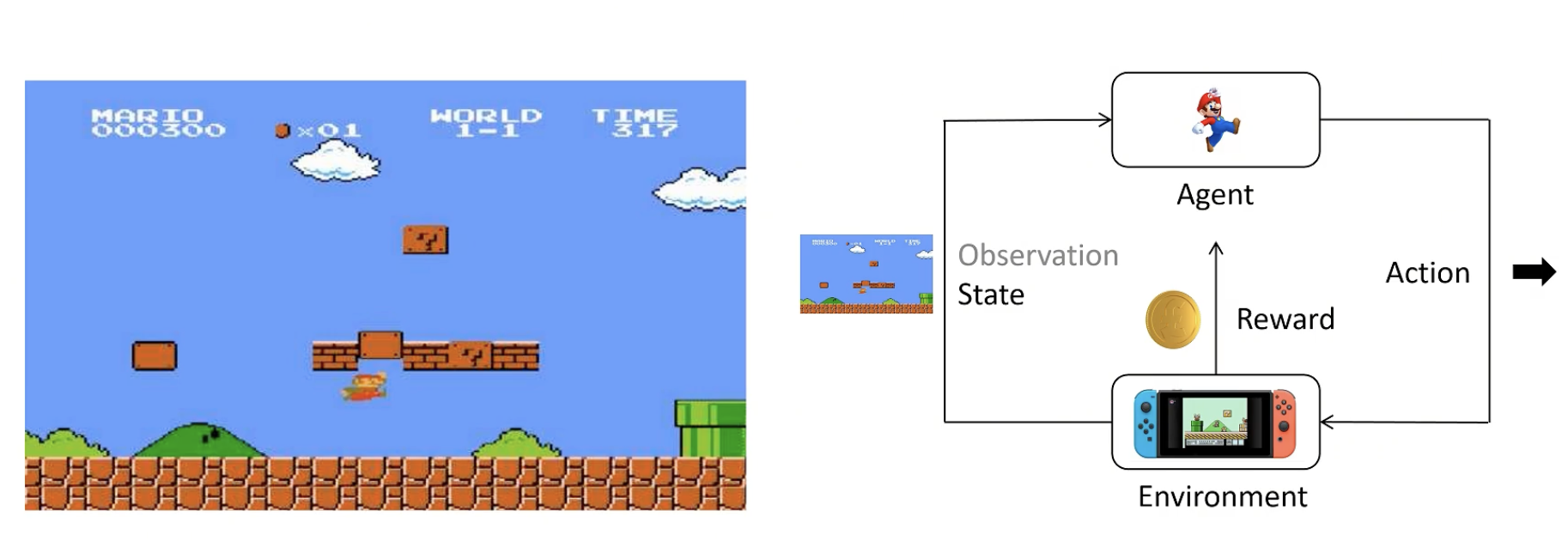
enviroment:看到的画面+看不到的后台画面,不了解细节
agent(智能体):根据策略得到尽可能多的奖励
state:当前状态
observation:state的一部分(有时候agent无法看全)
action:agent做出的动作
reward:agent做出一个动作后环境给予的奖励
action space:可以选择的动作,如上下左右
policy:策略函数,输入state,输出Action的概率分布。一般用π表示。
- 训练时应尝试各种action
- 输出应具有多样性
Trajectory/Episode/Rollout:轨迹,用 t 表示一连串状态和动作的序列。有的状态转移是确定的,也有的是不确定的。
Return:回报,从当前时间点到游戏结束的 Reward 的累积和。
强化学习目标:训练一个Policy神经网络π,在所有状态S下,给出相应的Action,得到Return的期望最大。
强化学习-数学基础
总述
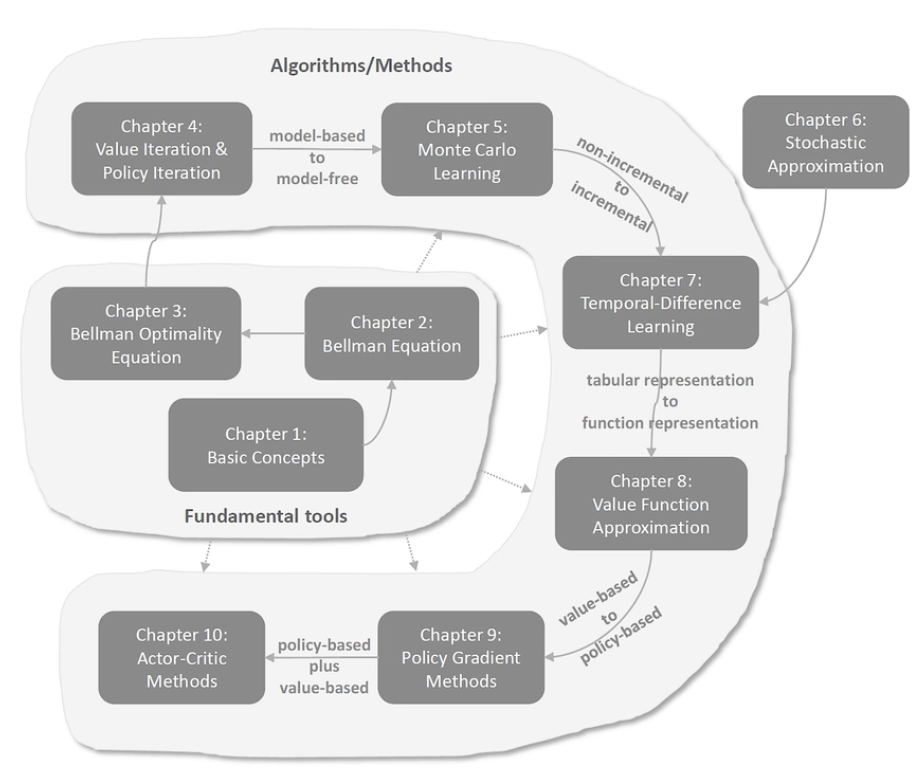
基础工具
- 基本概念:state, action, reward, return, episode, policy, mdp…
- 贝尔曼公式:用于评价策略
- 贝尔曼最优公式:强化学习的最终目标是求解最优策略
算法/方法
- 值迭代、策略迭代—— truncated policy iteration:值和策略update不断迭代
- Monte Carlo Learning:无模型学习
- 随即近似理论:from non-incremental to incremental
- 时序差分方法(TD)
- 值函数估计:tabular representation to function representation,引入神经网络
- Policy Gradient Methods:from value-based to policy-based
- Actor-Critic Methods:policy-based + value-based
强化学习-直观理解
不用告诉该怎么做,而是给定奖励函数,什么时候做好。
回归
增加折现因子
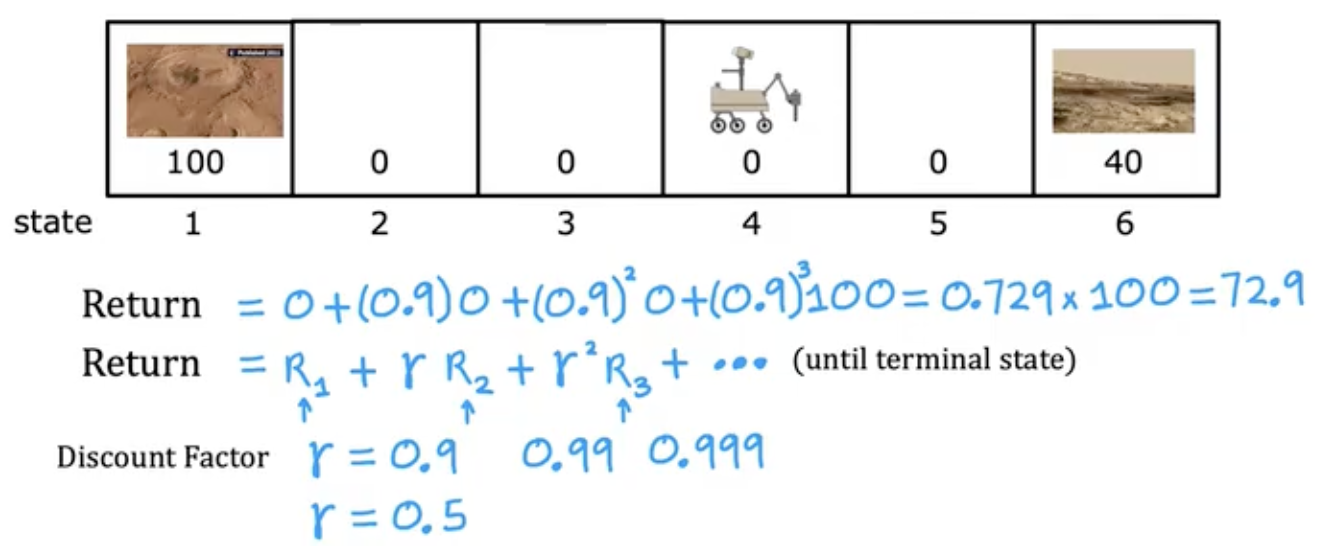
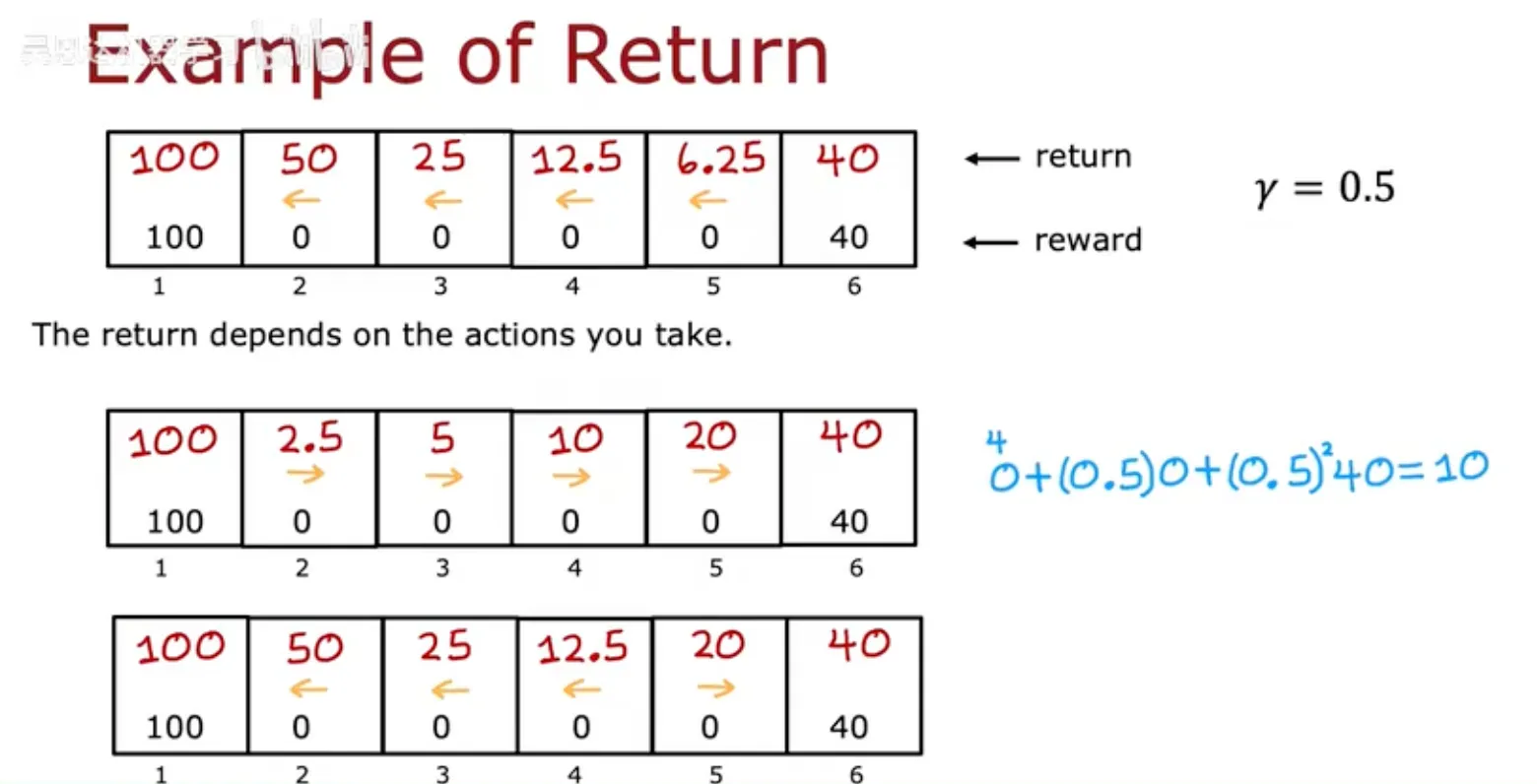
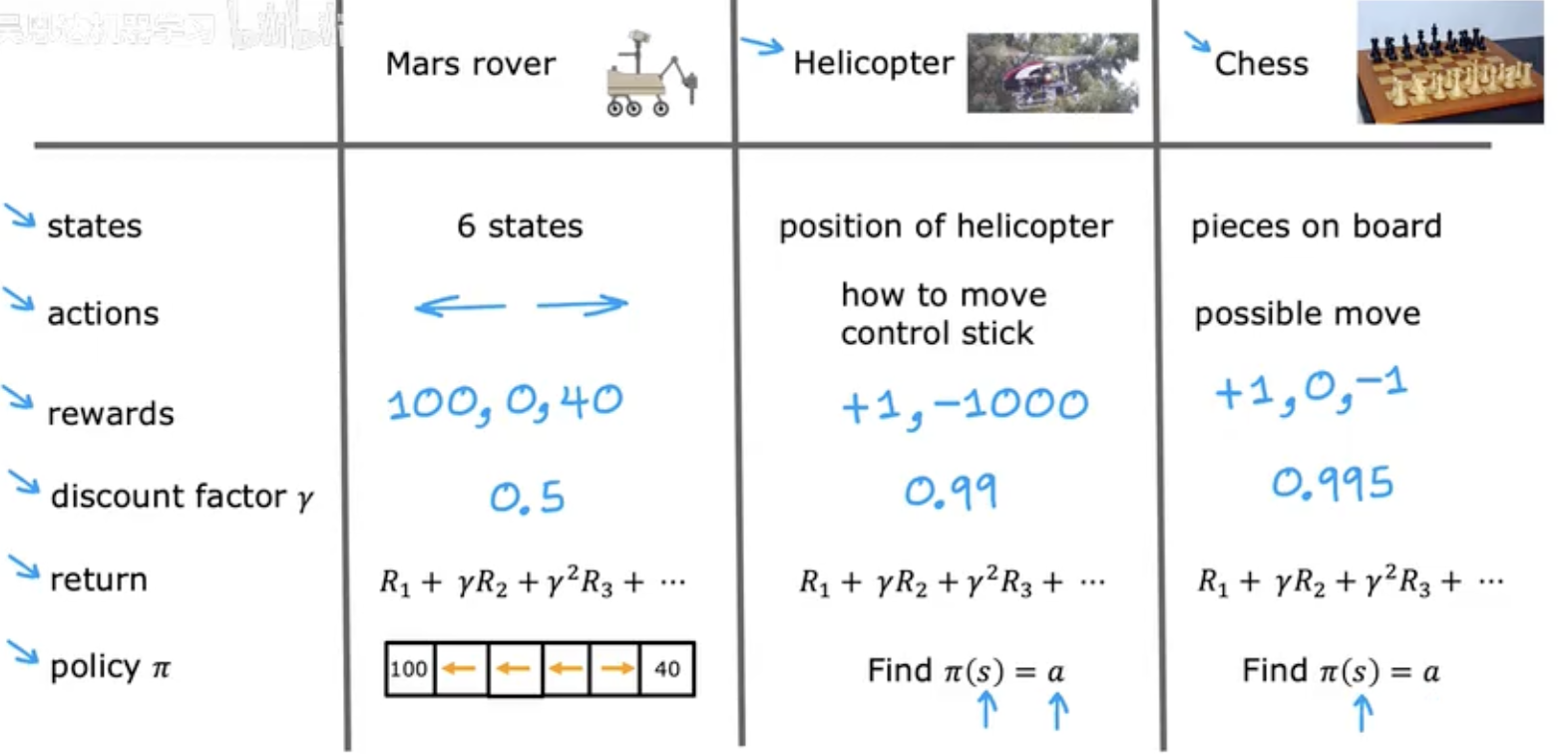
强化学习的形式化
A policy is a function $\pi(s) = a$ mapping from states to actions, that tells you what $action \space a$ to take in a given $state \space s$.
goal: Find a $policy \space \pi$ that tells you what $action (a = (s))$ to take in every $state (s)$ so as to maximize the return.
状态动作值函数(Q-Function)
Q(s,a) = Return if you:
- start in state s.
- take action a (once).
- then behave optimally after that.
The best possible return from state s is max$Q(s, a)$. The best possible action in state s is the action a that gives max$Q(s, a)$.








